题目内容
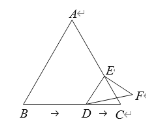
【题目】如图,在△ABC中,∠ACB=45°,点D在AB上,点E在AC的延长线上,ED⊥AB,ED交BC于点F,AB=DF,3DF=5EF,CF=l,则AC=_____.
【答案】![]()
【解析】
作GB⊥AB,GF⊥DE,GB与GF交于点G,连接GC、GE.四边形BDFG是矩形,去确定A、B、G、C四点共圆。得到FG=FE,又作HF⊥CF交CG于H,证明∴△GFH≌△EFC
再根据三角函数定义去设未知数求值即可.
如图,作GB⊥AB,GF⊥DE,GB与GF交于点G,连接GC、GE.
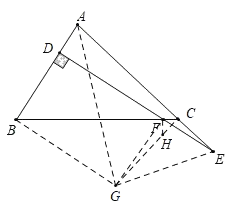
∵ED⊥AB于D,则四边形BDFG是矩形,
∴BG=DF,GF=BD,
∵AB=DF,
∴AB=BG,
∴∠AGB=45°,
∵∠ACB=45°,
∴∠ACB=∠AGB,
∴A、B、G、C四点共圆,
∴∠ACG=∠ABG=90°,∠GCB=∠ACB=45°,
∴∠GFE=∠GCE=90°,
∴G、F、C、E四点共圆,
∴∠FGC=∠FEC,∠FEG=∠FCG=45°,
∴FG=FE,
作HF⊥CF交CG于H,则∠CFH=∠GFE=90°,FC=FH,
∴∠GFH=∠EFC,
在△GFH和△EFC中:

∴△GFH≌△EFC(AAS),
∴GH=CE.
∵3DF=5EF,
∴3DF=5FG=5BD,
∴∠tan∠DFB=![]() =
=![]() ,
,
∴tan∠CGE=![]() =tan∠CFE=∠tan∠DFB=
=tan∠CFE=∠tan∠DFB=![]() ,
,
设CE=GH=3x,则CG=5x,所以CH=2x,
∵CF=1,
∴CH=![]() ,
,
∴2x=![]() ,
,
∴x=![]() ,
,
∴CG=5x=![]() ,
,
∵tan∠CAG=![]() =tan∠FBG=∠tan∠DFB=
=tan∠FBG=∠tan∠DFB=![]() ,
,
∴CA=![]() CG=
CG=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目