题目内容
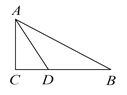
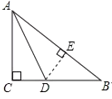
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,那么
,那么![]() 的长是 ____________.
的长是 ____________.
【答案】![]()
【解析】
过点D作DE⊥AB于点E由角平分线的性质得出DE=CD=BCBD=3cm=![]() BD,得出△ABD的面积=2△ACD的面积,证出AB=2AC,设AC=x(x>0),则AB=2x,由勾股定理得出方程,解方程即可.
BD,得出△ABD的面积=2△ACD的面积,证出AB=2AC,设AC=x(x>0),则AB=2x,由勾股定理得出方程,解方程即可.
解:如图,过点D作DE⊥AB于点E,
∵∠C=90°,AD平分∠CAB,
∴DE=CD=BCBD=3cm=![]() BD,
BD,
∴△ABD的面积=2△ACD的面积,
即![]() AB×DE=2×
AB×DE=2×![]() AC×CD,
AC×CD,
∴AB=2AC,
设AC=x(x>0),则AB=2x,
由勾股定理得:AC2+BC2=AB2,
即x2+92=(2x)2,
解得:x=3![]()
∴AB=2x=![]()
故答案为:![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
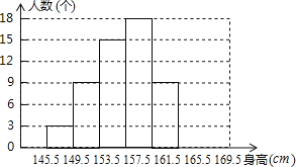
【题目】 为了解九年级女生的身高(单位:cm)情况,某中学对部分九年级女生身高进行了一次测量,所得数据整理后列出了频数分布表,并画了部分频数分布直方图(图、表如图):
分组 | 频数 | 频率 |
145.5-149.5 | 3 | 0.05 |
149.5-153.5 | 9 | n |
153.5-157.5 | m | 0.25 |
157.5-161.5 | 18 | 0.30 |
161.5-165.5 | 9 | 0.15 |
165.5-169.5 | 6 | 0.10 |
合计 | M | N |
根据以上图表,回答问题.
(1)M=______,m=______,N=______,n=______;
(2)补全频数分布直方图;
(3)若九年级有600名学生,则身高在161.5-165.5范围约为多少人?