题目内容
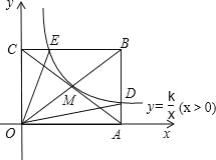
【题目】如图,反比例函数y=![]() (x>0)的图象经过矩形OABC对角线的交点M,分别交AB、BC于点D、E,连结DE.若四边形ODBE的面积为9,则△ODE的面积是________.
(x>0)的图象经过矩形OABC对角线的交点M,分别交AB、BC于点D、E,连结DE.若四边形ODBE的面积为9,则△ODE的面积是________.
【答案】![]()
【解析】
设B的坐标为(2a,2b),E点坐标为(x,2b),D点坐标为(2a,y),因为D、E、M在反比例函数图象上,则ab=k,2bx=k, 2ay=k, 根据四边形ODBE的面积列式,求得k值,再由2bx×2ay=4abxy=k2=9, 求得xy的值,然后根据所求的结果求出△BED的面积,则△ODE的面积就是四边形ODBE的面积和△BED的面积之差.
解:设B的坐标为(2a,2b), 则M点坐标为(a,b),
∵M在AC上,
∴ab=k(k>0),
设E点坐标为(x,2b),D点坐标为(2a,y),
则2bx=k, 2ay=k,
∴S四边形ODBE=2a×2b-![]() ×(2bx+2ay)=9,
×(2bx+2ay)=9,
即4k-![]() (k+k)=9,
(k+k)=9,
解得k=3,
∵2bx×2ay=4abxy=k2=9,
∴4abxy=9,
解得:xy=![]() ,
,
则S△BED=![]() BE×BD=
BE×BD=
![]() ,
,
∴S△ODE =S四边形ODBE -S△BED=9-![]()
![]()

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目