题目内容
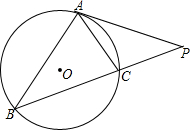
已知如图：△ABC内接于⊙O，P为BC边延长线上的一点，PA为⊙O的切线，切点为A，若PA=6，PC=4，求
的值．
| sinB |
| sinACB |
∵PA是⊙O的切线，
∴PA2=PC•PB，
∵PA=6，PC=4，
∴PB=9；
由弦切角定理知：∠PAC=∠ABC，
又∵∠APC=∠BPA，
∴△PAC∽△PBA，
∴
=
=
；
过A作⊙O的直径AD，连接BD、CD；
则有：∠ADB=∠ACB，∠ABC=∠ADC；
在Rt△ABD中，sinADB=sinACB=AB：AD，
同理得：sinADC=sinABC=AC：AD；
∴
=
=
．
∴PA2=PC•PB，
∵PA=6，PC=4，
∴PB=9；
由弦切角定理知：∠PAC=∠ABC，
又∵∠APC=∠BPA，
∴△PAC∽△PBA，
∴
| AB |
| AC |
| PB |
| PA |
| 3 |
| 2 |
过A作⊙O的直径AD，连接BD、CD；
则有：∠ADB=∠ACB，∠ABC=∠ADC；
在Rt△ABD中，sinADB=sinACB=AB：AD，
同理得：sinADC=sinABC=AC：AD；
∴
| sinB |
| sinACB |
| AC |
| AB |
| 2 |
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
m，0）且垂直于x轴，当P点在x轴上移动时，直线MN也随着平行移动．按下面条件求m的值或范围．
，交AY于点D．
CD的延长线的交点．
