题目内容
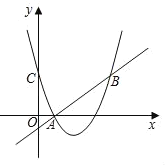
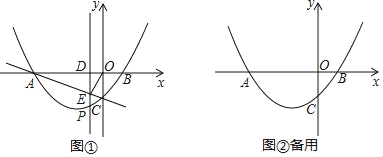
【题目】如图，抛物线y＝
与x轴分别交于A、B两点（点A在点B的左侧，）与y轴交于点C，作直线AC．
（1）点B的坐标为 ，直线AC的关系式为 ．
（2）设在直线AC下方的抛物线上有一动点P，过点P作PD⊥x轴于D，交直线AC于点E，当CE平分∠OEP时求点P的坐标．
（3）点M在x轴上，点N在抛物线上，试问以点A、C、M、N为顶点的四边形能否成为平行四边形？若存在，直接写出所有点M的坐标；若不存在，请简述你的理由．
【答案】（1）（2，0），y＝
x﹣4；（2）P（﹣
，﹣
）；（3）M的坐标为：（5+
，0）或（5﹣）或（﹣14，0）或（﹣2，0）．
【解析】
（1）令y=0，解关于x的一元二次方程即可求出点A、B的坐标，令x=0即可求出点C的坐标；根据待定系数法即可求出直线AC的解析式；
（2）先证明OE=OC=4，再设点E的坐标为（m，m﹣4），然后在Rt△ODE中根据勾股定理即可得出关于m的一元二次方程，解方程即可求出m的值，进一步即可求出结果；
（3）①当AC是平行四边形的边时，根据A到C的平移规律可得N（M）到M（N）的平移规律，解方程即可求得结果；②当AC是平行四边形的对角线时，利用中点坐标公式求解即可.
解：（1）y＝
，令y＝0，则
，解得x＝2或﹣8，令x＝0，则y＝﹣4，
所以点A、B、C的坐标分别为：（﹣8，0）、（2，0）、（0，﹣4），
将点A、C的坐标代入一次函数表达式：y＝kx+b得：
，解得：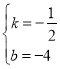
，
故直线AC的表达式为：y＝x﹣4；
故答案为：（2，0），y＝x﹣4；
（2）如图，∵CE平分∠OEP，∴∠OEC＝∠CEP，
∵PD∥y轴，∴∠CEP＝∠ECO＝∠OEC，∴OE=OC=4，
设点E的坐标为（m，m﹣4），
则在Rt△ODE中，根据勾股定理，得
，
解得：m＝﹣或0（不和题意，舍去），
由于P、E的横坐标相等，所以点P（﹣，﹣ ）；
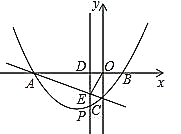
（3）设点M（s，0），N（m，n），则n＝
m2+
m﹣4，
①当AC是平行四边形的边时，
则点A向右平移8个单位，再向下平移4个单位得到C，
同理N（M）向右平移8个单位，再向下平移4个单位得到M（N），
即m+8＝s，n﹣4＝0或m﹣8＝s，n+4＝0，而n＝m2+m﹣4，
当m+8＝s，n﹣4＝0时，4＝m2+m﹣4，解得：
，所以s＝5±；
当m﹣8＝s，n+4＝0时，－4＝m2+m﹣4，解得：m=﹣6或0（舍去），所以s＝﹣14；
②当AC是平行四边形的对角线时，
利用中点坐标公式得：﹣8＝m+s，﹣4＝n，而n＝m2+m﹣4，解得：s＝﹣2；
综上，s＝5±或﹣14或﹣2；
故点M的坐标为：（5+，0）或（5﹣）或（﹣14，0）或（﹣2，0）．
