题目内容
8. 如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2
如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2(1)△BCD与△BAC相似吗?请说明理由.
(2)若CD=$\frac{5}{3}$,求AC的长.
分析 (1)利用两组对应边的比相等且夹角对应相等的两个三角形相似可判定△BCD∽△BAC;
(2)根据相似三角形的性质计算AC的长.
解答 解:(1)△BCD∽△BAC.理由如下:
∵BD=$\frac{4}{3}$,AB=3,BC=2,
∴$\frac{BD}{BC}$=$\frac{\frac{4}{3}}{2}$=$\frac{2}{3}$,$\frac{BC}{BA}$=$\frac{2}{3}$,
∴$\frac{BD}{BC}$=$\frac{BC}{BA}$,
而∠DBC=∠CBA,
∴△BCD∽△BAC;
(2)∵△BCD∽△BAC,
∴$\frac{CD}{AC}$=$\frac{BC}{BA}$,即$\frac{\frac{5}{3}}{AC}$=$\frac{2}{3}$,
∴AC=$\frac{5}{2}$.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.

练习册系列答案
相关题目
20.已知x=5是方程x-4+a=3的解,则a的值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
1.下列说法不正确的是( )
| A. | 两个有理数的和不一定大于每一个加数 | |
| B. | 任何有理数的绝对值都不小于0 | |
| C. | 最小的非负整数是0 | |
| D. | 一个数的绝对值等于它本身,则这个数是正数. |
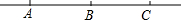 已知:A、B、C是一直线上顺次三点,并且BC=90.
已知:A、B、C是一直线上顺次三点,并且BC=90.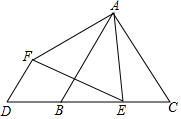 如图,点D在等边△ABC边CB的延长线上,点E是边BC上的动点,连结AE,在AE的左侧构造等边△AEF,连结DF,若DB=2,则DF的最小值是$\sqrt{3}$.
如图,点D在等边△ABC边CB的延长线上,点E是边BC上的动点,连结AE,在AE的左侧构造等边△AEF,连结DF,若DB=2,则DF的最小值是$\sqrt{3}$.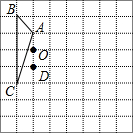 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤: