题目内容
19.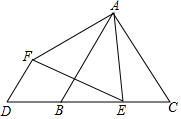 如图,点D在等边△ABC边CB的延长线上,点E是边BC上的动点,连结AE,在AE的左侧构造等边△AEF,连结DF,若DB=2,则DF的最小值是$\sqrt{3}$.
如图,点D在等边△ABC边CB的延长线上,点E是边BC上的动点,连结AE,在AE的左侧构造等边△AEF,连结DF,若DB=2,则DF的最小值是$\sqrt{3}$.
分析 根据题意得到点E在BC上移动,F在BN上移动,DF⊥BN时,DF最小,然后根据等边三角形的性质即可得到结论.
解答 解:当E在C点时,F落在B点上,当E在B点时,F落在N点上,
∴点E在BC上移动,F在BN上移动,
∴DF⊥BN时,DF最小,
则∠DBF=60°,
∵BD=2,
∴DF=$\sqrt{3}$.
∴DF的最小值是$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,平行线的判定,最短距离问题,证得△FNE≌△FBD是解决(2)的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
10.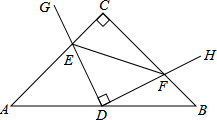 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
①AE+BF=$\frac{\sqrt{2}}{2}$AB,②△DEF始终为等腰直角三角形,
③S四边形CEDF=$\frac{1}{8}$AB2,
④AE2+CE2=2DF2.
其中正确的是( )
 在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:
在Rt△ABC中,AC=BC,点D为AB中点.∠GDH=90°,∠GDH绕点D旋转,DG、DH分别与边AC、BC交于E,F两点.下列结论:①AE+BF=$\frac{\sqrt{2}}{2}$AB,②△DEF始终为等腰直角三角形,
③S四边形CEDF=$\frac{1}{8}$AB2,
④AE2+CE2=2DF2.
其中正确的是( )
| A. | ①②③④ | B. | ①②③ | C. | ①④ | D. | ②③ |
11. 有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
 有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )| A. | b | B. | -b | C. | -2a-b | D. | 2a-b |
12.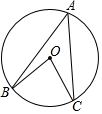 如图,点A、B、C在⊙O上,∠A=40°,则∠BOC=( )
如图,点A、B、C在⊙O上,∠A=40°,则∠BOC=( )
 如图,点A、B、C在⊙O上,∠A=40°,则∠BOC=( )
如图,点A、B、C在⊙O上,∠A=40°,则∠BOC=( )| A. | 40° | B. | 80° | C. | 60° | D. | 90° |
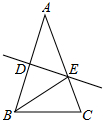 如图,在△ABC中,边AB的垂直平分线交AC于E,△ABC与△BEC的周长分别为24
如图,在△ABC中,边AB的垂直平分线交AC于E,△ABC与△BEC的周长分别为24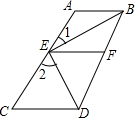 已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC,若∠1=32°.求∠2的度数.
已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC,若∠1=32°.求∠2的度数. 如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2
如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2