题目内容
3.在△ABC中,AB=2$\sqrt{3}$,AC=2,BC边上的高AD=$\sqrt{3}$,如果有一个正方形的一边在AB上,另外两个顶点分别为AC,BC上,则这个正方形的边长是3-$\sqrt{3}$或$\frac{12-2\sqrt{3}}{11}$.分析 根据条件显然有两种情况,由相似三角形的性质和勾股定理即可得出结果.
解答 解:根据条件显然有两种情况,如图,
(1)在图(1)中,BC=4时,可求CD=1,∠CAD=30°,
∴∠B=30°,∠C=60°,
∴△ABC是直角三角形,
∴BC=4.
设正方形边长为x,如图(3)所示:
∵$\frac{EG}{AC}=\frac{BE}{AB}$,
∴$\frac{x}{2}$=$\frac{2\sqrt{3}-x}{2\sqrt{3}}$,
解得x=3-$\sqrt{3}$;
(2)在图(2)中,可求CD=1,∠CAD=30°,∠B=30°
∴∠BAD=60°,△ABC是等腰三角形,AC平分∠BAD,
BC=AC=2.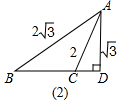
在图(4)中,当BC=2时,
∵AC=2,
∴△ABC是等腰三角形,
此时内接正方形h是△ABC的AB边上的高,
h=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,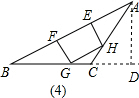
设正方形边长为x,由△HGC∽△ABC得,$\frac{HG}{AB}=\frac{hx}{h}$,即
$\frac{x}{2\sqrt{3}}=\frac{1-x}{x}$,
解得x=$\frac{12-2\sqrt{3}}{11}$;
故答案为:3-$\sqrt{3}$或$\frac{12-2\sqrt{3}}{11}$.
点评 本题考查了相似三角形的判定和性质,等腰三角形的判定和性质,勾股定理,掌握的作出图形是解题的关键.

练习册系列答案
相关题目
11. 有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
 有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )
有理数a、b在数轴上的位置如图所示,则化简|a-b|+a的结果为( )| A. | b | B. | -b | C. | -2a-b | D. | 2a-b |
16.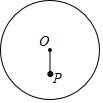 如图,⊙O的半径为10,若OP=8,则经过点P的弦长可能是( )
如图,⊙O的半径为10,若OP=8,则经过点P的弦长可能是( )
 如图,⊙O的半径为10,若OP=8,则经过点P的弦长可能是( )
如图,⊙O的半径为10,若OP=8,则经过点P的弦长可能是( )| A. | 10 | B. | 6 | C. | 19 | D. | 22 |
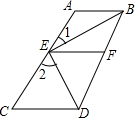 已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC,若∠1=32°.求∠2的度数.
已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC,若∠1=32°.求∠2的度数. 如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2
如图,D是△ABC的边AB上的一点,BD=$\frac{4}{3}$,AB=3,BC=2