题目内容
在平面直角坐标系xOy中,抛物线 与x轴交于A、B两点(点A在点B的左侧),点B的坐标为
与x轴交于A、B两点(点A在点B的左侧),点B的坐标为 ,与y轴交于点
,与y轴交于点 ,顶点为D。
,顶点为D。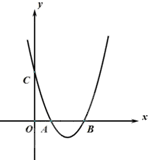
(1)求抛物线的解析式及顶点D坐标;
(2)联结AC、BC,求∠ACB的正切值;
(1)y=(x-2)2-1,D(2,-1);(2) .
.
解析试题分析:(1)把点B与点C的坐标代入抛物线解析式,利用待定系数法求解,把解析式整理成顶点式即可写出顶点坐标;
(2)首先得出A点坐标,进而得出∠OBC=45°,BC=3 ,再过点A作AH⊥BC,垂足为H,利用tAn∠ACB=
,再过点A作AH⊥BC,垂足为H,利用tAn∠ACB= 求出即可.
求出即可.
试题解析: (1)∵抛物线过点B(3,0),点C(0,3),
∴ ,解得
,解得 ,
,
∴抛物线解析式为:y=x2-4x+3,
又∵y=x2-4x+3=(x-2)2-1,
∴顶点D的坐标是:D(2,-1);
(2)∵抛物线y=x2-4x+3与x轴交于点A、B两点(点A在B点的左侧),
∴A(1,0),
又∵O(0,0),C(0,3),B(3,0),
∴BO=CO=3,
∵∠COB=90°,
∴∠OBC=45°,BC=3 ,
,
过点A作AH⊥BC,垂足为H,
∴∠AHB=90°,
∵AB=2,∴AH=BH= ,
,
∴CH=BC-BH=2 ,
,
∴tAn∠ACB= .
.
考点: 二次函数综合题.

练习册系列答案
相关题目
 x2+1,点C的坐标为(-4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
x2+1,点C的坐标为(-4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.


 与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
与x轴交于A、B两点,点C是抛物线在第一象限内部分的一个动点,点D是OC的中点,连接BD并延长,交AC于点E.
 ;
; 的面积为
的面积为 时,求
时,求 的值.
的值.
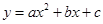 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD= .
.