题目内容
如图,在平面直角坐标系中,抛物线经过A(-1,0),B(4,0),C(0,-4),⊙M是△ABC的外接圆,M为圆心。
⑴求抛物线的解析式;
⑵求阴影部分的面积;
⑶在正半轴上有一点P,作PQ⊥x轴交BC于Q,设PQ=K,△CPQ的面积为S,求S关于K的函数关系式,并求出S的最大值。
(1)y==x2-3x-4;(2) ;(3)S=-
;(3)S=- k2+2k,2.
k2+2k,2.
解析试题分析:(1)已知了A、B、C三点坐标可用待定系数法求出抛物线的解析式.
(2)要求扇形的面积需要知道半径的长和扇形的圆心角的度数,先求圆心角∠AMC的度数,由于OB=OC,因此∠ABC=45°,根据圆周角定理可得出∠AMC=90°.再求半径,由于三角形AMC是等腰直角三角形,因此半径的平方等于AC的平方的一半,可在直角三角形OAC中求出AC的平方,据此可根据扇形的面积公式求出扇形的面积.
(3)求三角形CPQ的面积可以PQ为底,以OP为高,已知了PQ=k,在等腰直角三角形BPQ中,BP=PQ=k,也就能表示长OP的长,据此可求出S与k的函数关系,根据函数的性质即可求出S的最大值.
试题解析:(1)由抛物线经过A(-1,0),B(4,0),
设抛物线的解析式为:y=a(x+1)(x-4),
将C(0,-4)代入上式中,得-4a=-4,a=1.
∴y=(x+1)(x-4)=x2-3x-4.
(2)∵A(-1,0),B(4,0),C(0,-4).
∴OB=OC=4,OA=1
∴∠OBC=45°,∴∠AMC=90°
∴AM2+MC2=OA2+OC2=12+42=17
∴AM2=CM2= ,
,
∴S阴影= .
.
(3)∠OBC=45°,PQ⊥x轴;
∴BP=PQ=k,
∴S= k•(4-k)=-
k•(4-k)=- k2+2k.
k2+2k.
∴当k=2时,S最大值=2.
考点: 二次函数综合题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 与x轴交于A、B两点(点A在点B的左侧),点B的坐标为
与x轴交于A、B两点(点A在点B的左侧),点B的坐标为 ,与y轴交于点
,与y轴交于点 ,顶点为D。
,顶点为D。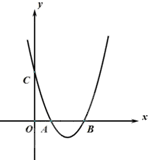
 与
与 轴相交于A、B两点,与
轴相交于A、B两点,与 轴相交于点C,若已知B点的坐标为B(8,0).
轴相交于点C,若已知B点的坐标为B(8,0).
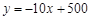 .
. (b,c是常数,且c<0)与
(b,c是常数,且c<0)与 轴分别交于点A、B(点A位于点B的左侧),与
轴分别交于点A、B(点A位于点B的左侧),与 轴的负半轴交于点C,点A的坐标为(-1,0).
轴的负半轴交于点C,点A的坐标为(-1,0).
 .求抛物线的解析式.
.求抛物线的解析式. 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.
 与坐标轴交于
与坐标轴交于 三点,点
三点,点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线 与
与 轴交于点
轴交于点 ,点
,点 是线段
是线段 上的一个动点,
上的一个动点, 于点
于点 .若
.若 ,且
,且 .
.
 的值
的值 的坐标(其中
的坐标(其中 用含
用含 的式子表示):
的式子表示): 为等腰三角形?
为等腰三角形? 元,此时的销售量是多少?(用含
元,此时的销售量是多少?(用含