题目内容
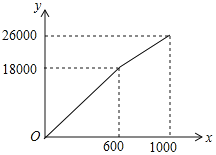
【题目】为了创建“全国文明城市”,鄂州市积极主动建设美丽家园,某社区拟将一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草面积为x(m2),种草费用y1(元)与x(m2)的函数关系式为y1=![]() ,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系如表所示:
x(m2) | 100 | 200 | 300 |
y2(元) | 3900 | 7600 | 11100 |
(1)请直接写出y1与种草面积x(m2)的函数关系式,y2与栽花面积x(m2)的函数关系式;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与种草面积x(m2)的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于600m2,栽花部分的面积不少于200m2,请求出绿化总费用W的最小值.
【答案】(1)y1=![]() ,y2=-0.01x2+40x;(2)32500元;(3)x=800时,w有最小值29600元.
,y2=-0.01x2+40x;(2)32500元;(3)x=800时,w有最小值29600元.
【解析】
(1)函数y1是一次函数,函数y2是二次函数,利用待定系数法即可解决问题;
(2)分两种情形构建二次函数,利用二次函数的性质即可解决问题;
(3)求出自变量x的取值范围,利用二次函数的性质即可解决问题;
解:(1)y1=![]() ,y2=-0.01x2+40x;
,y2=-0.01x2+40x;
(2)当0≤x<600时,W=y1+y2=30x+[-0.01(1000-x)2+40(1000-x)]
=-0.01x2+10x+30000
=-0.01(x-500)2+32500
∵-0.01<0,
∴x=500时,w有最大值32500.
当600≤x≤1000时,w=y1+y2=20x+6000+[-0.01(1000-x)2+40(1000-x)]
=-0.01x2+36000,
∵-0.01<0,
∴当600≤x≤1000时,w随x的增大而减小,
∴当x=600时,w有最大值32400,
综上所述,绿化总费用W的最大值为32500元.
(3)由题意:![]() ,解得600≤x≤800,
,解得600≤x≤800,
∵600≤x≤800时,w=-0.01x2+36000,w随x的增大而减小,
∴x=800时,w有最小值29600元.

 阅读快车系列答案
阅读快车系列答案