题目内容
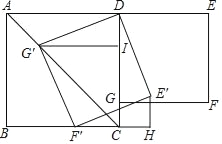
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】试题解析:作G′I⊥CD于I,G′R⊥BC于R,E′H⊥BC交BC的延长线于H.连接RF′.则四边形RCIG′是正方形.
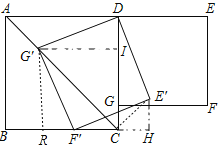
∵∠DG′F′=∠IGR=90°,∴∠DG′I=∠RG′F′,在△G′ID和△G′RF中,∵G′D= G′F,∠D G′I=∠R G′F′,G′I= G′R,∴△G′ID≌△G′RF,∴∠G′ID=∠G′RF′=90°,∴点F′在线段BC上,在Rt△E′F′H中,∵E′F′=2,∠E′F′H=30°,∴E′H=![]() E′F′=1,F′H=
E′F′=1,F′H=![]() ,易证△RG′F′≌△HF′E′,∴RF′=E′H,RG′RC=F′H,∴CH=RF′=E′H,∴CE′=
,易证△RG′F′≌△HF′E′,∴RF′=E′H,RG′RC=F′H,∴CH=RF′=E′H,∴CE′=![]() ,∵RG′=HF′=
,∵RG′=HF′=![]() ,∴CG′=
,∴CG′=![]() RG′=
RG′=![]() ,∴CE′+CG′=
,∴CE′+CG′=![]() .
.
故选A.

练习册系列答案
相关题目