��Ŀ����
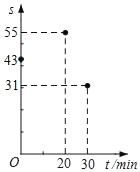
����Ŀ����ͼ�����������ţ���������ˮ��8mʱ��ˮ���ABΪ12m����ˮ������6mʱ�ﵽ����ˮλ����ʱ�����ڵ�ˮ������Ƕ���m��
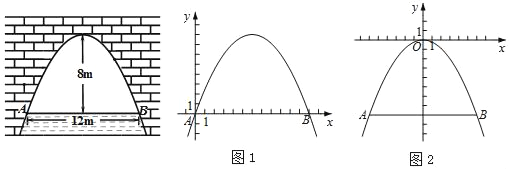
��������˽�������������ַ������벹��������
����һ����ͼ1���Ե�AΪԭ�㣬AB����ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵxOy��
��ʱ��B������Ϊ���� ������ �����������ߵĶ�������Ϊ���� ������ ������
������������������ʾ�Ķ��κ����Ľ���ʽΪ�� ����
��y��6ʱ�������ʱ�Ա���x��ȡֵ�����ɽ��������⣮
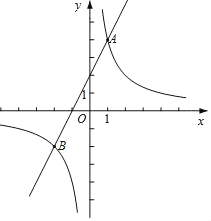
����������ͼ2���������߶���Ϊԭ�㣬�Գ���Ϊy�ᣬ����ƽ��ֱ������ϵxOy��
��ʱ��������������ʾ�Ķ��κ����Ľ���ʽΪ�� ����
��y���� ��ʱ�������ʱ�Ա���x��ȡֵΪ�� �������ɽ��������⣮
���𰸡�12��0��6��8��y����![]() x2+
x2+![]() x��y����
x��y����![]() x2����2����3��
x2����2����3��
��������
����һ�������������ʿɵó�B��O���꣬Ȼ������κ����Ľ���ʽΪy��a��x��6��2��8�ٽ�B��������뼴�ɵõ�a��ֵ.
������������κ����Ľ���ʽΪy��ax2��B����뼴�ɵõ�a��ֵ����y����2ʱ���������ʽ���������.
�⣺����һ��B��12��0����O��6��8����
����κ����Ľ���ʽΪy��a��x��6��2��8��
��B����������ã�a����![]() ��
��
����κ����Ľ���ʽΪy����![]() x2��
x2��![]() x��
x��
������������κ����Ľ���ʽΪy��ax2��
��B��6����8������ã�a����![]() ��
��
����κ����Ľ���ʽΪy����![]() x2��
x2��
y����2ʱ�������ʱ�Ա���x��ȡֵΪ��3��
�ʴ�Ϊ��12��0��6��8��y����![]() x2��
x2��![]() x��y����
x��y����![]() x2����2����3��
x2����2����3��

 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�