题目内容
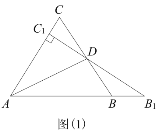
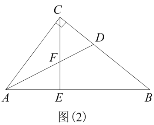
【题目】如图，点
在线段
上，在的同侧作等腰
和等腰
，
与
、
分别交于点
、
.对于下列结论：
①
；②
；③
.其中正确的是（ ）
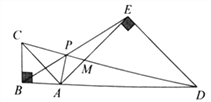
A. ①②③ B. ① C. ①② D. ②③
【答案】A
【解析】（1）由等腰Rt△ABC和等腰Rt△ADE三边份数关系可证；
（2）通过等积式倒推可知，证明△PAM∽△EMD即可；
（3）2CB2转化为AC2，证明△ACP∽△MCA，问题可证．
由已知：AC=
AB，AD=AE
∴
∵∠BAC=∠EAD
∴∠BAE=∠CAD
∴△BAE∽△CAD
所以①正确
∵△BAE∽△CAD
∴∠BEA=∠CDA
∵∠PME=∠AMD
∴△PME∽△AMD
∴
∴MPMD=MAME
所以②正确
∵∠BEA=∠CDA
∠PME=∠AMD
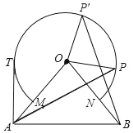
∴P、E、D、A四点共圆
∴∠APD=∠EAD=90°
∵∠CAE=180°-∠BAC-∠EAD=90°
∴△CAP∽△CMA
∴AC2=CPCM
∵AC=AB
∴2CB2=CPCM
所以③正确
故选A．
练习册系列答案
名校课堂系列答案
相关题目
