题目内容
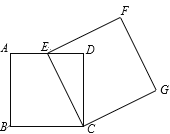
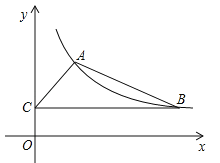
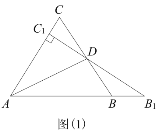
【题目】如图(1)所示,等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于点C1交AB的延长线于点B1.
(1)请你探究:![]() =
=![]() ,
,![]() =
=![]() 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问![]() =
=![]() 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
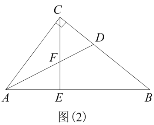
(3)如图(2)所示Rt△ABC中,∠ACB=90°,AC=8,AB=![]() ,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求
,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求![]() 的值.
的值.
【答案】(1)两个等式都成立.理由见解析; (2)结论仍然成立,理由见解析;(3) ![]() =
=![]() .
.
【解析】
(1)根据等边三角形的性质得到AD垂直平分BC,∠CAD=∠BAD=30°,AB=AC,则DB=CD,易得![]() ;由于∠C1AB1=60°,得∠B1=30°,则AB1=2AC1,同理可得到DB1=2DC1,易得
;由于∠C1AB1=60°,得∠B1=30°,则AB1=2AC1,同理可得到DB1=2DC1,易得![]() ;
;
(2)过B点作BE∥AC交AD的延长线于E点,根据平行线的性质和角平分线的定义得到∠E=∠CAD=∠BAD,则BE=AB,并且根据相似三角形的判定得△EBD∽△ACD,得到![]() ,而BE=AB,于是有
,而BE=AB,于是有![]() ,这实际是三角形的角平分线定理;
,这实际是三角形的角平分线定理;
(3)AD为△ABC的内角角平分线,由(2)的结论得到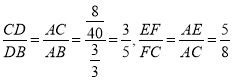 ,又
,又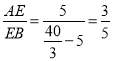 ,则有
,则有![]() ,得到DE∥AC,根据相似三角形的判定得△DEF∽△ACF,即有
,得到DE∥AC,根据相似三角形的判定得△DEF∽△ACF,即有![]() .
.
解:(1)两个等式都成立.理由如下:
∵△ABC为等边三角形,AD为角平分线,
∴AD垂直平分BC,∠CAD=∠BAD=30°,AB=AC,
∴DB=CD,
∴![]() =
=![]() ,
,
∵∠C1AB1=60°,
∴∠B1=30°,
∴AB1=2AC1,
又∠DAB1=30°,
∴DA=DB1,
而DA=2DC1,
∴DB1=2DC1,
∴![]() =
=![]() ;
;
(2)结论仍然成立,理由如下:
如图所示,
△ABC为任意三角形,过B点作BE∥AC交AD的延长线于E点,
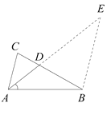
∴∠E=∠CAD=∠BAD,
∴BE=AB,
∵BE∥AC,
∴△EBD∽△ACD,
∴![]() =
=![]() ,
,
而BE=AB,
∴![]() =
=![]() .
.
(3)如图,连接DE,
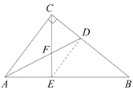
∵AD为△ABC的内角角平分线,
∴![]() =
=![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
又![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴DE∥AC,
∴△DEF∽△ACF,
∴![]() =
=![]() =
=![]() .
.

【题目】为了了解同学们对垃圾分类知识的了解程度,增强同学们的环保意识,某校数学兴趣小组设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试.根据测试成绩分布情况,将测试成绩分成A、B、C、D四组,绘制了如下统计图表:
![]()
组别 | 分数/分 |
A | 60<x≤70 |
B | 70<x≤80 |
C | 80<x≤90 |
D | 90<x≤100 |
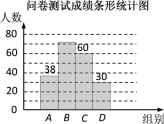
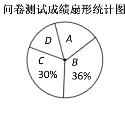
请结合以上信息解答下列问题:
(1)本次抽样调查的样本总量是多少?
(2)样本中,测试成绩在B组的频数是多少,在D组的频率是多少?
(3)样本中,这次测试成绩的中位数落在哪一组?
(4)如果该校共有800名学生,请估计成绩在90<x≤100的学生约有多少人?