题目内容
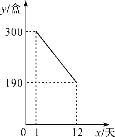
【题目】某公司开发出一款新包装的牛奶，牛奶的成本价为6元/盒，这种新包装的牛奶在正式投放市场前通过代销点进行了为期一个月(30天)的试营销，售价为8元/盒．前几天的销量每况愈下，工作人员对销售情况进行了跟踪记录，并将记录情况绘成图象，图中的线段表示前12天日销售量y(盒)与销售时间x(天)之间的函数关系，于是从第13天起采用打折销售(不低于成本价)，时间每增加1天，日销售量就增加10盒．
（1）打折销售后，第17天的日销售量为________盒；
（2）求y与x之间的函数关系式，并写出x的取值范围；
（3）已知日销售利润不低于560元的天数共有6天，设打折销售的折扣为a折，试确定a的最小值．
【答案】（1）240；（2）y＝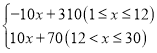
；（3）9.5
【解析】
（1）由图像可得第12天的日销售量为190盒，因为从第13天起采用打折销售(不低于成本价)，时间每增加1天，日销售量就增加10盒，故日销售量比第12天增加50盒，为240盒；
（2）当1≤x≤12时，令y＝kx＋b，代入x＝1时，y＝300；x＝12，y＝190即可求解；当12<x≤30时，则y＝190＋10(x－12)，化简即可；
（3）先计算出当1≤x≤12时，有三天日销售利润不低于560元，确定当12<x≤30时，有三天日销售利润不低于560元，由函数的增减性即可求解．
（1）由图像可得第12天的日销售量为190盒，因为从第13天起采用打折销售(不低于成本价)，时间每增加1天，日销售量就增加10盒，故日销售量比第12天增加50盒，为240盒；
故答案为：240
（2）当1≤x≤12时，
令y＝kx＋b．
由图知：当x＝1时，y＝300；x＝12，y＝190．
∴
∴
∴y＝—10x＋310(1≤x≤12)．
当12<x≤30时，y＝190＋10(x－12)．
∴y＝10x＋70 (12<x≤30)．
∴y＝
（3）当1≤x≤12时，
由(8－6)y≥560得， 2(－10x＋310)≥560，
解得： x≤3．
∴1≤x≤3，x＝1，2，3，共三天．
∵日销售利润不低于560元的天数共有6天，
∴当12<x≤30时，有三天日销售利润不低于560元，
由y＝10x＋70 (28<x≤30)得y随x的增大而增大，
∵x为整数，∴x＝28，29，30时，日销售利润不低于560元，且当x＝28时，利润最低．
由题意得，(8×0.1a－6)(10×28＋70)≥560．
∴a≥9.5，
∴a的最小值为9.5．
