题目内容
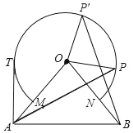
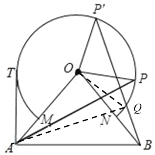
【题目】如图,△OAB中,OA=OB=10cm,∠AOB=80°,以点O为圆心,半径为6cm的优弧![]() 分别交OA、OB于点M、N.
分别交OA、OB于点M、N.
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′.求证:AP=BP′;
(2)点T在左半弧上,若AT与圆弧相切,求AT的长.
(3)Q为优弧上一点,当△AOQ面积最大时,请直接写出∠BOQ的度数为 .
【答案】(1)证明见解析;(2)AT=8;(3)170°或者10°.
【解析】
(1)欲证明AP=BP′,只要证明△AOP≌△BOP′即可;
(2)在Rt△ATO中,利用勾股定理计算即可;
(3)当OQ⊥OA时,△AOQ面积最大,且左右两半弧上各存在一点分别求出即可.
解:(1)证明:∵∠AOB=∠POP′=80°
∴∠AOB+∠BOP=∠POP′+∠BOP即∠AOP=∠BOP′
在△AOP与△BOP′中
 ,
,
∴△AOP≌△BOP′(SAS),
∴AP=BP′;
(2)∵AT与弧相切,连结OT,
∴OT⊥AT
在Rt△AOT中,根据勾股定理,
AT=![]()
∵OA=10,OT=6,
∴AT=8;
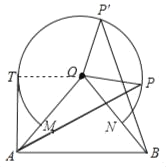
(3)解:如图,当OQ⊥OA时,△AOQ的面积最大;
理由是:
当Q点在优弧MN左侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ+∠AOB=90°+80°=170°,
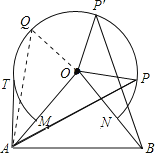
当Q点在优弧MN右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ-∠AOB=90°-80°=10°,
综上所述:当∠BOQ的度数为10°或170°时,△AOQ的面积最大.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目