题目内容
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

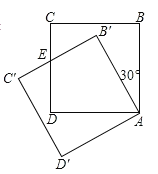
(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B=____.
(问题解决)
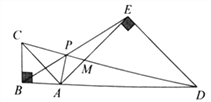
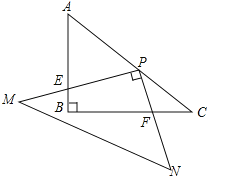
(3)如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
【答案】(1)如图,△AB′C′即为所求;见解析;(2)45°;(3)S△APC=![]() .
.
【解析】
(1)如图所示,△AB′C′即为所求;
(2)利用等腰三角形的性质即可解决问题;
【问题解决】
结论:PA2+PB2=PC2.
证法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
证法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.
(1)如图,△AB′C′即为所求;
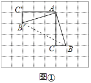
(2)∵△ABB′是等腰直角三角形,
∴∠AB′B=45°.
故答案为45°;
(3)如图②,

∵将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,
∴△APP′是等边三角形,∠AP′C=∠APB=360°﹣90°﹣120°=150°,
∴PP′=AP,∠AP′P=∠APP′=60°,∴∠PP′C=90°,∠P′PC=30°,
∴PP′= ![]() PC,即AP=
PC,即AP= ![]() PC
PC
∵∠APC=90°,∴AP2+PC2=AC2 , 即(![]() PC)2+PC2=72 , ∴PC=
PC)2+PC2=72 , ∴PC=![]() ,
,
∴AP=![]() ,∴S△APC=
,∴S△APC=![]() APPC=
APPC=![]()