题目内容
【题目】某运输公司派出大小两种型号共20辆渣土运输车运输士方．已知一辆大型渣土运输车和两辆小型渣土运输车每次共运20吨；3辆大型渣土运输车和8辆小型渣土运输车每次共运70吨．并且一辆大型渣土运输车运输花费500元/次，一辆小型渣土运输车运输花费300元/次．
（1）一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨？
（2）若每次运输主方总不小于148吨，且小型渣土运输车至少派出7辆，问该渣土运输公司有哪几种派出方案？最少需要花费多少元？
【答案】（1）一辆大型渣土运输车每次运土方10吨，一辆小型渣土运输车每次运土方5吨；（2）见解析
【解析】
（1）设一辆大型渣土运输车每次运土方x吨，一辆小型渣土运输车每次运土方y吨，根据等量关系，列出二元一次方程组，即可求解；
（2）设小型渣土运输车派出m辆，则大型渣土运输车派出（20-m）辆，根据题意，列出关于m的不等式组，求出m的范围，再取整数，即可得到结论．
（1）设一辆大型渣土运输车每次运土方x吨，一辆小型渣土运输车每次运土方y吨，
依题意，得：
，解得：
．
答：一辆大型渣土运输车每次运土方10吨，一辆小型渣土运输车每次运土方5吨；
（2）设小型渣土运输车派出m辆，则大型渣土运输车派出（20-m）辆，
依题意，得：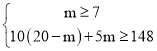
，
解得：7≤m≤10.4，
∵m为整数，
∴m=7，8，9，10．
∴该渣土运输公司有4种排出方案，方案1：派出大型渣土运输车13辆，小型渣土运输车7辆；方案2：派出大型渣土运输车12辆，小型渣土运输车8辆；方案3：派出大型渣土运输车11辆，小型渣土运输车9辆；方案4：派出大型渣土运输车10辆，小型渣土运输车10辆．
方案1所需总费用为500×13+300×7=8600（元）；
方案2所需总费用为500×12+300×8=8400（元）；
方案3所需总费用为500×11+300×9=8200（元）；
方案4所需总费用为500×10+300×10=8000（元）．
∵8600＞8400＞8200＞8000，
∴派出大型渣土运输车和小型渣土运输车各10辆花费最少，最少花费为8000元．
