题目内容
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B=__________.
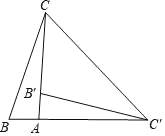
【答案】77°
【解析】
先根据旋转的性质得∠B=∠AB′C′,AC=AC′,∠CAC′=90°,则可判断△ACC′为等腰直角三角形,所以∠ACC′=∠AC′C=45°,然后根据三角形外角性质计算出∠AB′C′,从而得到∠B的度数.
∵△ABC绕点A顺时针旋转90°后得到的△AB′C′,
∴∠B=∠AB′C′,AC=AC′,∠CAC′=90°,
∴△ACC′为等腰直角三角形,
∴∠ACC′=∠AC′C=45°,
∴∠AB′C′=∠B′CC′+∠CC′B′=45°+32°=77°,
∴∠B=77°.
故答案为77°.

练习册系列答案
相关题目
【题目】下表是今年雨季某河流一周的水位变化情况(上周末的水位达到警戒水位)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位记录 |
|
|
|
|
|
|
|
注:此河流的警戒水位为![]() 米.
米.
![]() 完成下面的本周水位变化记录表:
完成下面的本周水位变化记录表:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
|
|
|
(注:规定水位比前一天上升用“![]() ”,水位比前一天下降用“
”,水位比前一天下降用“![]() ”,不升不降记作“
”,不升不降记作“![]() ”.)
”.)
![]() 与上周末相比,本周末河流水位是上升了还是下降了? (填“上升”或“下降”)
与上周末相比,本周末河流水位是上升了还是下降了? (填“上升”或“下降”)