题目内容
【题目】定义:若两个三角形,有两边相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为偏差三角形.
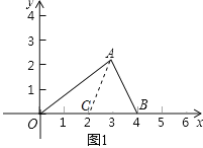
(1)如图1,已知A(3,2),B(4,0),请在x轴上找一个C,使得△OAB与△OAC是偏差三角形.你找到的C点的坐标是______,直接写出∠OBA和∠OCA的数量关系______.
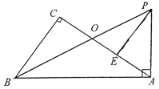
(2)如图2,在四边形ABCD中,AC平分∠BAD,∠D+∠B=180°,问△ABC与△ACD是偏差三角形吗?请说明理由.
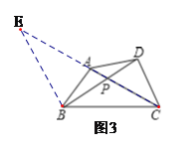
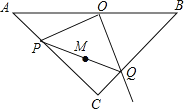
(3)如图3,在四边形ABCD中,AB=DC,AC与BD交于点P,BD+AC=9,∠BAC+∠BDC=180°,其中∠BDC<90°,且点C到直线BD的距离是3,求△ABC与△BCD的面积之和.

【答案】(1)(2,0),∠OBA+∠OCA=180°;(2)△ABC与△ACD是偏差三角形,理由见解析;(3)![]()
【解析】
(1)根据偏差三角形的定义,即可得到C的坐标,根据等腰三角形的性质和平角的定义,即可得到结论;
(2)在AD上取一点H,使得AH=AB,易证△CAH≌△CAB,进而可得∠D=∠CHD,根据偏差三角形的定义,即可得到结论;
(3)延长CA至点E,使AE=BD,连接BE,由SAS可证BDCEAB,得EA=BD,点B到直线EA的距离是3,根据三角形的面积公式,即可求解.
(1)∵当AC=AB时,△OAB与△OAC是偏差三角形,A(3,2),B(4,0),
∴点C的坐标为(2,0),如图1,
∵AC=AB,
∴∠ACB=∠ABC,
∵∠OCA+∠ACB=180°,
∴∠OBA+∠OCA=180°,
故答案为:(2,0),∠OBA+∠OCA=180°;
(2)△ABC与△ACD是偏差三角形,理由如下:
如图2中,在AD上取一点H,使得AH=AB.
∵AC平分∠BAD,
∴∠CAH=∠CAB,
又∵ AC=AC,
∴△CAH≌△CAB(SAS),
∴CH=CB,∠B=∠AHC,
∵∠B+∠D=180°,∠AHC+∠CHD=180°,
∴∠D=∠CHD,
∴CH=CD,
∴CB=CD,
∵△ACD和△ABC中,AC=AC,∠CAD=∠CAB,BC=CD,△ADC与△ABC不全等,
∴△ABC与△ACD是偏差三角形;
(3)如图3中, 延长CA至点E,使AE=BD,连接BE,
∵∠BAC+∠BDC=180°,∠BAC+∠BAE=180°,
∴∠BDC=∠BAE,
又∵AB=CD,
∴BDCEAB(SAS),
∴EA=BD,
∵点C到直线BD的距离是3,
∴点B到直线EA的距离是3,
∴S△ABC+S△BCD=S△ABC+S△EAB= S△BCE=![]() (AC+EA)×3 =
(AC+EA)×3 =![]() (AC+BD)×3 =
(AC+BD)×3 =![]() ×9×3=
×9×3=![]() .
.