题目内容
【题目】已知,△ABC 中,∠BAC=90°,AB=AC,过 A 任作一直线 l,作 BD⊥l于 D,CE⊥l于 E,观察三条线段 BD,CE,DE 之间的数量关系.
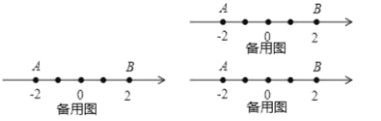
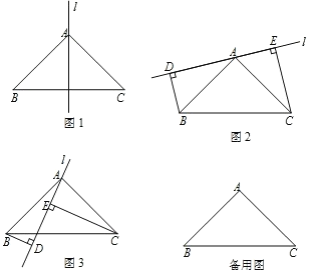
(1)如图 1,当 l 经过 BC 中点时,此时 BD CE;
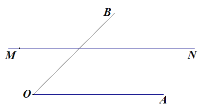
(2)如图 2,当 l 不与线段 BC 相交时,BD,CE,DE 三者的数量关系为 ,并证明 你的结论.
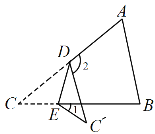
(3 )如图 3 ,当 l 与线段 BC 相交,交点靠近 B 点时,BD ,CE ,DE 三者的数量关系 为 .证明你的结论,并画图直接写出交点靠近 C 点时,BD,CE,DE 三者的数最关 系为 .
【答案】(1)=;(2)DE=BD+CE,理由详见解析;(3)CE﹣BD=DE,BD﹣CE=DE,理由详见解析.
【解析】
(1)由等腰三角形的性质可得直线![]() ,可得点
,可得点![]() ,点
,点![]() 与
与![]() 的中点重合,即
的中点重合,即![]() ;
;
(2)如图2,由“![]() ”可证
”可证![]() ,可得
,可得![]() ,
,![]() ,可得
,可得![]() ;
;
(3)如图3,由“![]() ”可证
”可证![]() ,可得
,可得![]() ,
,![]() ,可得
,可得![]() ,如图4,由“
,如图4,由“![]() ”可证
”可证![]() ,可得
,可得![]() ,
,![]() ,可得
,可得![]() .
.
解:(1)![]() ,
,![]() ,
,![]() 经过
经过![]() 中点
中点
![]() 直线
直线![]() ,
,
![]() 点
点![]() ,点
,点![]() 与
与![]() 的中点重合,
的中点重合,
![]()
故答案为:![]()
(2)如图![]() ,
,
理由如下:
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,且
,且![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
故答案为:![]() ,
,
(3)如图![]()
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,且
,且![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
![]()
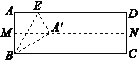
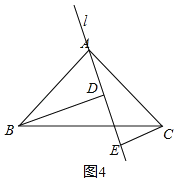
如图4,若交点靠近![]() 点时,
点时,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,且
,且![]() ,
,![]() ,
,
![]()
![]() ,
,![]()
![]() .
.
故答案为:![]() ,
,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目