题目内容
【题目】对一张矩形纸片ABCD进行折叠,具体操作如下:
第一步:先对折,使AD与BC重合,得到折痕MN,展开;
第二步:再一次折叠,使点A落在MN上的点A′处,并使折痕经过点B,得到折痕BE,同时,得到线段BA′,EA′,展开,如图1;
第三步:再沿EA′所在的直线折叠,点B落在AD上的点B′处,得到折痕EF,同时得到线段B′F,展开,如图2.
求证:(1)∠ABE=30°;
(2)四边形BFB′E为菱形.
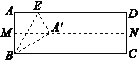

图1 图2
【答案】(1)30°;(2)见解析
【解析】
(1)由折叠的性质易得:∠ABE=∠A′BE,M是AB的中点,A′是EF的中点,∠EA′B=∠A=90°,由此可得BA′是EF的垂直平分线,从而可得BE=BF,由此可得∠A′BE=∠A′BF,从而可得∠ABE=∠A′BE=∠A′BF,这样结合∠ABC=90°即可得到∠ABE=![]() ∠ABC=30°;
∠ABC=30°;
(2)由已知条件结合折叠的性质可得:BE=B′E,BF=B′F,这样结合(1)中所得BE=BF即可得到四边形BFB′E的四边相等,由此即可得到四边形BFB′E是菱形.
(1)∵对折使AD与BC重合,折痕是MN,
∴M是AB的中点,
∴A′是EF的中点.
∵∠BA′E=∠A=90°,
∴BA′垂直平分EF,
∴BE=BF,
∴∠A′BE=∠A′BF.
由翻折的性质,知∠ABE=∠A′BE,
∴∠ABE=∠A′BE=∠A′BF,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() ×90°=30°;
×90°=30°;
(2)∵沿EA′所在的直线折叠,
点B落在AD上的点B′处,
∴BE=B′E,BF=B′F.
∵BE=BF,
∴BE=B′E=B′F=BF,
∴四边形BFB′E为菱形.

练习册系列答案
相关题目