题目内容
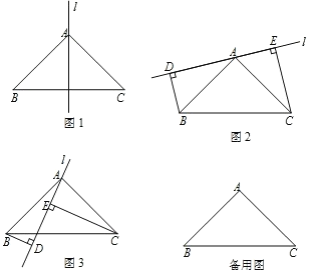
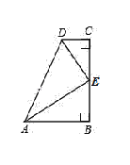
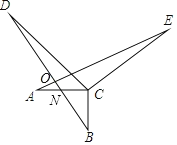
【题目】如图,AC⊥BC,DC⊥EC,AC=BC,DC=EC,图中AE、BD有怎样的关系(数量关系和位置关系)?并证明你的结论.

【答案】结论:AE=BD,AE⊥BD,证明见解析.
【解析】
只要证明△DCB≌△ECA(SAS),推出∠A=∠B,BD=AE由∠AND=∠BNC,∠B+∠BNC=90°推出∠A+∠AND=90°,可得∠AON=90°由此即可解决问题.
结论:AE=BD,AE⊥BD.理由如下:
如图,设AC交BD于N,AE交BD于O.
∵AC⊥BC,DC⊥EC,∴∠ACB=∠DCE=90°,∴∠DCB=∠ECA.
在△DCB和△ECA中,∵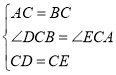 ,∴△DCB≌△ECA(SAS),∴∠A=∠B,BD=AE.
,∴△DCB≌△ECA(SAS),∴∠A=∠B,BD=AE.
∵∠AND=∠BNC,∠B+∠BNC=90°,∴∠A+∠AND=90°,∴∠AON=90°,∴BD⊥AE.

练习册系列答案
相关题目