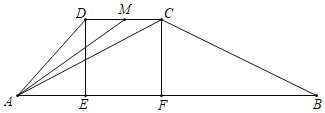
题目内容
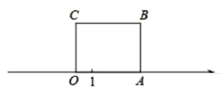
【题目】已知数轴上两点![]() 、
、![]() ,其中A表示的数为-2,
,其中A表示的数为-2,![]() 表示的数为2,若在数轴上存在一点
表示的数为2,若在数轴上存在一点![]() ,使得
,使得![]() ,则称点
,则称点![]() 叫做点
叫做点![]() 、
、![]() 的“
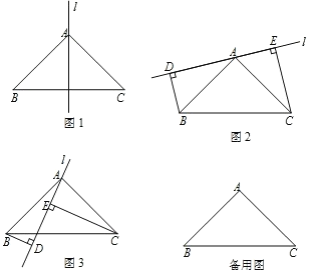
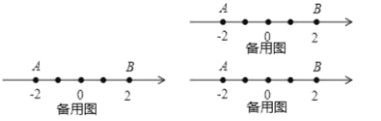
的“![]() 节点”,例如图1所示,若点
节点”,例如图1所示,若点![]() 表示的数为0,有
表示的数为0,有![]() ,则称点
,则称点![]() 为点
为点![]() 、
、![]() 的“4节点”.
的“4节点”.
请根据上述规定回答下列问题:
(1)若点![]() 为点
为点![]() 、
、![]() 的“
的“![]() 节点”,且点
节点”,且点![]() 在数轴上表示的数为-4,求
在数轴上表示的数为-4,求![]() 的值.
的值.
(2)若点![]() 是数轴上点
是数轴上点![]() 、
、![]() 的“5节点”,请你直接写出点
的“5节点”,请你直接写出点![]() 表示的数为____________;
表示的数为____________;
(3)若点![]() 在数轴上(不与
在数轴上(不与![]() 、
、![]() 重合),满足
重合),满足![]() 、
、![]() 之间的距离是
之间的距离是![]() 、
、![]() 之间距离的一半,且此时点
之间距离的一半,且此时点![]() 为点
为点![]() 、
、![]() 的“
的“![]() 节点”,求
节点”,求![]() 的值.
的值.
【答案】(1)8;(2)![]() ;(3)4或12
;(3)4或12
【解析】
(1)利用"n节点"的概念进行解答即可;
(2)设点D表示的数为x,由"5节点"的定义列出方程分情况进行解答;
(3)根据点E的不同位置:①当点E在BA延长线上时;②当点E在线段AB上时;③当点E在AB延长线上时,根据BE=![]() AE,先求点E表示的数,再根据AC+BC=n,列方程解答即可.
AE,先求点E表示的数,再根据AC+BC=n,列方程解答即可.
解:(1)由A表示的数为-2,B表示的数为2,点C在数轴上表示的数为-4,
∴AC=2,BC=6,
∴n=AC+BC-2+6=8.
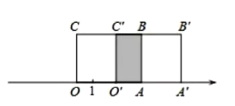
(2)如图:
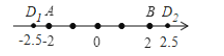
∵点D是数轴上点A、B的“5节点"
∴AC+BC=5,
∵AB=4
∴C在点A的左侧或在点A的右侧,
设点D表示的数为x,则AC+BC=5,
∴-2-x+2-x=5或x-2+x-(-2)=5,x=-2.5或2.5,
则点D表示的数为2.5或-2.5;
(3) 根据点E和BE的位置关系,需分三种情况:
①当点E在BA延长线上时,BE不可能等于![]() AE,故舍弃;
AE,故舍弃;
②当点E在线段AB上时,满足BE=![]() AE,如图:
AE,如图:
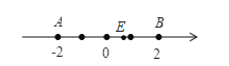
∴n=AE+BE=AB=4;
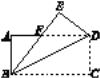
③当点E在AB延长线上时,如图:
![]()
∵BE=![]() AE
AE
∴BE=AB=4,
∴点E表示的数为6,
则n=AE+BE=8+4=12
所以 n=4或n=12.