题目内容
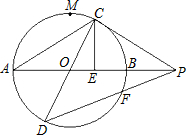 如图,已知AB=2,AB、CD是⊙O的两条直径,M为弧AB的中点,C在弧MB上运动,点P在AB的延长上,且PC=AC,作CE⊥AP于E,连接DP交⊙O于F.
如图,已知AB=2,AB、CD是⊙O的两条直径,M为弧AB的中点,C在弧MB上运动,点P在AB的延长上,且PC=AC,作CE⊥AP于E,连接DP交⊙O于F.(1)求证:当AC=
| 3 |
(2)在PC与⊙O相切的条件下,求sin∠APD的值?
分析:(1)连接BC,AB为直径,解直角三角形ABC得∠A=30°,又PC=AC,得∠CPE=∠A=30°,∠COP=∠A+∠ACO=2∠A=60°,利用内角和定理证明∠OCP=90°;
(2)作DH⊥AP垂足为H,可证DH=CE,利用解直角三角形求CE,在Rt△CDP中,由CD=2,CP=
,利用勾股定理求DP,由sin∠APD=
求解.
(2)作DH⊥AP垂足为H,可证DH=CE,利用解直角三角形求CE,在Rt△CDP中,由CD=2,CP=
| 3 |
| DH |
| DP |
解答: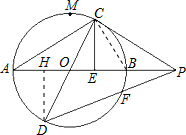 (1)证明:连接BC,
(1)证明:连接BC,
∵AB为直径,
∴∠ACB=90°,
在Rt△ABC中,cosA=
=
,
∴∠A=30°,
又∵PC=AC,
∴∠CPE=∠A=30°,
∴∠COP=∠A+∠ACO=2∠A=60°,
∴∠OCP=180°-∠CPE-∠COP=90°,
∴PC与⊙O相切;
(2)解:在Rt△CDP中,
∵CD=2,CP=
∴DP=
(1分)
作DH⊥AP垂足为H(1分)
∵∠HOD=∠COE,OC=OD,∠CEO=∠DHO=90°,
∴Rt△DHO≌Rt△CEO(1分)
可得DH=CE=AC•sin30°=
(1分)
在Rt△DHP中:sin∠APD=
=
=
 (1)证明:连接BC,
(1)证明:连接BC,∵AB为直径,
∴∠ACB=90°,
在Rt△ABC中,cosA=
| AC |
| AB |
| ||
| 2 |
∴∠A=30°,
又∵PC=AC,
∴∠CPE=∠A=30°,
∴∠COP=∠A+∠ACO=2∠A=60°,
∴∠OCP=180°-∠CPE-∠COP=90°,
∴PC与⊙O相切;
(2)解:在Rt△CDP中,
∵CD=2,CP=
| 3 |
∴DP=
| 7 |
作DH⊥AP垂足为H(1分)
∵∠HOD=∠COE,OC=OD,∠CEO=∠DHO=90°,
∴Rt△DHO≌Rt△CEO(1分)
可得DH=CE=AC•sin30°=
| ||
| 2 |
在Rt△DHP中:sin∠APD=
| DH |
| DP |
| ||||
|
| ||
| 14 |
点评:本题考查了切线的判定,全等三角形的判定与性质,勾股定理,圆周角定理,解直角三角形的知识.关键是作辅助线,将问题转化到特殊三角形中求解.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
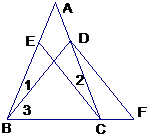 24、如图,已知AB=AC,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由.
24、如图,已知AB=AC,∠1=∠2,∠3=∠F,试判断EC与DF是否平行,并说明理由.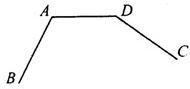 17、(保留作图痕迹)如图,已知AB=DC.
17、(保留作图痕迹)如图,已知AB=DC.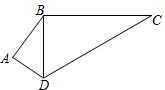 如图,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD.判断BC⊥BD吗?简述你的理由.
如图,已知AB=4,BC=12,CD=13,DA=3,AB⊥AD.判断BC⊥BD吗?简述你的理由.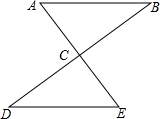 如图:已知AB∥DE,点C是AE的中点,
如图:已知AB∥DE,点C是AE的中点,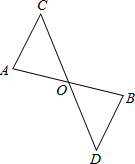 如图,已知AB、CD交于点O,且点O是AB的中点,AC∥BD,请说明点O是CD的中点的理由.
如图,已知AB、CD交于点O,且点O是AB的中点,AC∥BD,请说明点O是CD的中点的理由.