题目内容
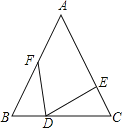
【题目】如图，△ABC中，AB＝AC，BD＝CE，BF＝CD，若∠A＝50°，则∠EDF的度数是（ ）
A.75°B.70°C.65°D.60°
【答案】C
【解析】
根据等腰三角形的性质可得出∠B=∠C及∠B的度数，结合BD=CE、BF=CD，即可证出△BDF≌△CED（SAS），由全等三角形的性质可得出∠CDE=∠BFD，再根据三角形内角和定理及平角等于180°，即可得出∠EDF=∠B，此题得解．
解：∵AB=AC，∠A=50°，
∴∠B=∠C=
（180°﹣∠A）=65°．
在△BDF和△CED中，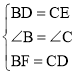
，
∴△BDF≌△CED（SAS），
∴∠CDE=∠BFD．
∵∠BDF+∠BFD+∠B=180°，∠BDF+∠EDF+∠CDE=180°，
∴∠EDF=∠B=65°．
故选：C．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
