题目内容
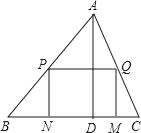
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
【答案】矩形的长为6cm,宽为4cm;或长为![]() cm,宽为
cm,宽为![]() cm.
cm.
【解析】试题分析:由已知可得 BC∥PQ,从而有△APQ∽△ABC,继而可得![]() ,由于矩形长与宽的比为3:2,分两种情况分别求解即可.
,由于矩形长与宽的比为3:2,分两种情况分别求解即可.
试题解析:
∵四边形PQMN是矩形,
∴BC∥PQ,
∴△APQ∽△ABC,
∴![]() ,
,
由于矩形长与宽的比为3:2,
∴分两种情况:
①若PQ为长,PN为宽,
设PQ=3k,PN=2k,
则![]() ,
,
解得:k=2,
∴PQ=6cm,PN=4cm;
②PN为6,PQ为宽,
设PN=3k,PQ=2k,
则![]() ,
,
解得:k=![]() ,
,
∴PN=![]() cm,PQ=
cm,PQ=![]() cm;
cm;
综上所述:矩形的长为6cm,宽为4cm;或长为![]() cm,宽为
cm,宽为![]() cm.
cm.


练习册系列答案
相关题目