题目内容
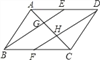
【题目】已知:r如图,在梯形ABCD中,AD∥BC,∠BCD=90°.对角线AC、BD相交于点E。且AC⊥BD。(1)求证:CD=BC·AD;(2)点F是边BC上一点,连接AF,与BD相交于点G,如果∠BAF=∠DBF,求证:![]() 。
。

【答案】见解答过程.
【解析】
试题(1)首先根据已知得出∠ACD=∠CBD,以及∠ADC=∠BCD=90°,进而求出△ACD∽△DBC,即可得出答案;
(2)首先证明△ABG∽△DBA,进而得出AG:AD=AB:BD,再利用△ABG∽△DBA,得出BG:AB="AB:BD" ,则AB2=BGBD,进而得出答案.
试题解析:证明:(1)∵AD∥BC,∠BCD=90°,
∴∠ADC=∠BCD=90°,
又∵AC⊥BD,∴∠ACD+∠ACB=∠CBD+∠ACB=90°,
∴∠ACD=∠CBD,
∴△ACD∽△DBC,
∴AD CD ="CD" BC ,
即CD2=BC×AD;
(2)∵AD∥BC,∴∠ADB=∠DBF,
∵∠BAF=∠DBF,∴∠ADB=∠BAF,
∵∠ABG=∠DBA,∴△ABG∽△DBA,
∴S△ABG:S△DBA =(![]() )2=AG2:AD2,
)2=AG2:AD2,
而S△ABG:S△DBA="BG:BD" ,∴AG2:AD2 ="BG:BD" .

练习册系列答案
相关题目