题目内容
12.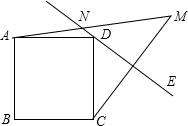 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
分析 根据对称的性质可知,NC=NM,DC=DM,推出∠NCD=∠NMD=∠DAM,推出∠ANC=90°,求出AC即可解决问题.
解答 解:如图所示,连接CN、DM、AC,
∵点C关于直线DE的对称点为M,
∴CN=MN,CD=DM,
∴∠NCM=∠NMC,∠DCM=∠DMC,
∴∠DCN=∠DMN,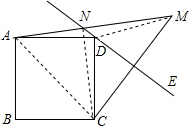
在正方形ABCD中,AD=CD,
∴AD=DM,
∴∠DAM=∠DMN,
∴∠DCN=∠DAM,
∵∠ACN+∠CAN=∠BCD-∠DCN+∠CAD+∠DAM=∠BCD+∠CAD=90°,
∴∠ANC=180°-90°=90°,
∴△ACN是直角三角形,
∴AC=$\sqrt{A{N}^{2}+C{N}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴正方形ABCD的边长=$\frac{\sqrt{2}}{2}$AC=$\frac{5\sqrt{2}}{2}$.
故选D.
点评 本题考查正方形的性质、轴对称的性质、勾股定理等知识,解题的关键是发现△ANC是直角三角形,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
 如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
20.已知圆锥的母线长为5cm,高为4cm,则这个圆锥的侧面积为( )
| A. | 12π cm2 | B. | 15π cm2 | C. | 20π cm2 | D. | 25π cm2 |
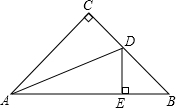 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AB=10cm,AC=BC=5$\sqrt{2}$cm,则△DBE的周长等于10cm.
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E,若AB=10cm,AC=BC=5$\sqrt{2}$cm,则△DBE的周长等于10cm.
 如图,已知在△ABC中,∠A=90°.
如图,已知在△ABC中,∠A=90°.