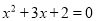题目内容
19.用一个半径为6的扇形作一个圆锥的侧面,这个圆锥的底面画圆的半径为2,则这个扇形的圆心角为120°.分析 根据题意可以求得扇形的弧长,然后跟扇形的弧长公式与圆心角的关系,求得这个扇形的圆心角.
解答 解:由题意可得,
扇形的弧长为:2π×2=4π,
设扇形的圆心角为n°,
则$\frac{nπ×6}{180}$=4π,
解得,n=120,
故答案为:120°.
点评 本题考查圆锥的计算,解题的关键是明确圆锥展开图扇形的弧长计算公式.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
12. 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
11.下列判断正确的是( )
| A. | x2-5$\sqrt{x}$+4=0是一元二次方程 | |
| B. | ax2+bx+c=0是一元二次方程 | |
| C. | 一元二次方程ax2+bx+c=0(a≠0)的二次项是a | |
| D. | 一元二次方程ax2+bx+c=0(a≠0)的常数项是c |
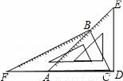
 的一元二次方程的两个根为
的一元二次方程的两个根为 ,
,  ,则这个方程是( )
,则这个方程是( )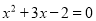 B.
B. 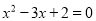
 D.
D.