题目内容
19.三角形的三条边的长为整数,且两两不等,最长边为8,这样的三角形共有9个.分析 根据最长边为8可知另一条边的长为7,6,5,4,3,2,1共7种情况,再根据三角形的三边关系进行讨论即可.
解答 解:∵三角形的三条边的长为整数,且两两不等,最长边为8,
∴当另一条边的长度为7时,设第三边为a,
则8-7<a<8+7,即1<a<15,
∴a=2,3,4,5,6,7共6种情况;
当另一条边的长度为6时,设第三边为a,
则8-6<a<8+6,即2<a<14,
∴a=3,4,5,6,7共5种情况;
当另一条边的长度为5时,设第三边为a,
则8-5<a<8+5,即3<a<13,
∴a=4,5,6,7共4种情况;
当另一条边的长度为4时,设第三边为a,
则8-4<a<8+4,即4<a<12,
∴a=5,6,7共3种情况;
当另一条边的长度为3时,设第三边为a,
则8-3<a<8+3,即5<a<11,
∴a=6,7共2种情况;
当另一条边的长度为2时,设第三边为a,
则8-2<a<8+2,即6<a<10,
∴a=7,共1种情况;
当另一条边的长度为1时,设第三边为a,
则8-1<a<8+1,即7<a<9,不合题意.
∴共有6+5+4+3+2+1=21种情况,重复计算的有12种,
∴这样的三角形共有21-12=9个.
故答案为:9.
点评 本题考查的是三角形的三边关系,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目
12.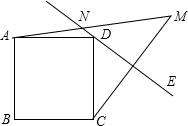 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
8.有一种记分的方法:80分以上如88分记为+8分,某个学生在记分表上记为-6分,则这个学生的分数应该是( )分.
| A. | 74 | B. | -74 | C. | 86 | D. | -86 |
4.-( $\frac{1}{2}$-$\frac{1}{3}$)的相反数是( )
| A. | -$\frac{1}{2}$-$\frac{1}{3}$ | B. | -$\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$-$\frac{1}{3}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$ |
11.下列判断正确的是( )
| A. | x2-5$\sqrt{x}$+4=0是一元二次方程 | |
| B. | ax2+bx+c=0是一元二次方程 | |
| C. | 一元二次方程ax2+bx+c=0(a≠0)的二次项是a | |
| D. | 一元二次方程ax2+bx+c=0(a≠0)的常数项是c |
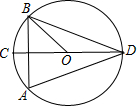 如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )
如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )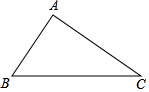 如图,已知在△ABC中,∠A=90°.
如图,已知在△ABC中,∠A=90°.