题目内容
3. 如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 连接BC,根据切线长定理得到PA=PB,然后根据等腰三角形的性质求得∠PAB的度数,根据切线的性质得∠PAO=90°,则∠BAC即可求得,然后利用直径所对的圆周角是直角,以及直角三角形的性质求解.
解答  解:连接BC.
解:连接BC.
∵PA、PB切⊙O于A、B两点,
∴PA=PB,AC⊥PA,即∠PAC=90°,
∴∠PAB=∠PBA=$\frac{180°-∠P}{2}$=$\frac{180°-40°}{2}$=70°,
∵∠BAC=∠PAC-∠PAB=90°-70°=20°,
∵AC是直径,
∴∠ABC=90°,
∴∠ACB=90°-∠ACB=90°-20°=70°.
故选C.
点评 本题考查了切线的性质以及等腰三角形的性质,已知圆的切线常用的辅助线是连接圆心和切点.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
16.下列分解因式正确的是( )
| A. | x3-x=x(x2-1) | B. | m2+m-7=(m+3)(m-2)-1 | C. | (a+4)(a-4)=a2-16 | D. | x2-y2=(x+y)(x-y) |
15.下列变形正确的是( )
| A. | 若x=y,则x-a=y+a | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则$\frac{a}{{c}^{2}}$=$\frac{b}{{c}^{2}}$ | ||
| C. | 若ac2=bc2,则a=b | D. | 若x=y,则$\frac{x}{a+2}$=$\frac{y}{a+2}$ |
12.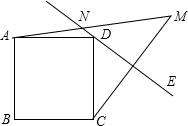 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
11.下列判断正确的是( )
| A. | x2-5$\sqrt{x}$+4=0是一元二次方程 | |
| B. | ax2+bx+c=0是一元二次方程 | |
| C. | 一元二次方程ax2+bx+c=0(a≠0)的二次项是a | |
| D. | 一元二次方程ax2+bx+c=0(a≠0)的常数项是c |
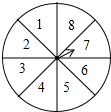 如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向小于6的数的概率为$\frac{5}{8}$.
如图,转盘中8个扇形的面积都相等,任意转动转盘1次,当转盘停止转动时,指针指向小于6的数的概率为$\frac{5}{8}$.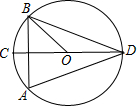 如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )
如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )