题目内容
20.已知圆锥的母线长为5cm,高为4cm,则这个圆锥的侧面积为( )| A. | 12π cm2 | B. | 15π cm2 | C. | 20π cm2 | D. | 25π cm2 |
分析 首先根据勾股定理求得底面半径,则可以得到底面周长,然后利用扇形的面积公式即可求解.
解答 解:底面半径是:$\sqrt{{5}^{2}-{4}^{2}}$=3,则底面周长是6π,
则圆锥的侧面积是:$\frac{1}{2}$×6π×5=15π.
故选B.
点评 考查了圆锥的计算.正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
15.下列变形正确的是( )
| A. | 若x=y,则x-a=y+a | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则$\frac{a}{{c}^{2}}$=$\frac{b}{{c}^{2}}$ | ||
| C. | 若ac2=bc2,则a=b | D. | 若x=y,则$\frac{x}{a+2}$=$\frac{y}{a+2}$ |
5.(-$\frac{5}{13}$)2015×(-2$\frac{3}{5}$)2016的值是( )
| A. | -1 | B. | 1 | C. | -$\frac{13}{5}$ | D. | $\frac{5}{13}$ |
12.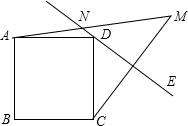 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
 如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )
如图,在正方形ABCD外侧作直线DE,点C关于直线DE的对称点为M,连接CM,AM.其中AM交直线DE于点N.若45°<∠CDE<90°,则当MN=4,AN=3时,正方形ABCD的边长为( )| A. | $\sqrt{7}$ | B. | 5 | C. | 5$\sqrt{2}$ | D. | $\frac{5}{2}$$\sqrt{2}$ |
8.有一种记分的方法:80分以上如88分记为+8分,某个学生在记分表上记为-6分,则这个学生的分数应该是( )分.
| A. | 74 | B. | -74 | C. | 86 | D. | -86 |
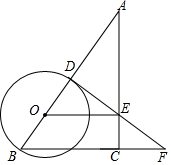 如图,在Rt△ABC中,∠ACB=90°,点O是AB上的动点,⊙O过点B交AB于点D,OE⊥AC,垂足为E,DE的延长线交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,点O是AB上的动点,⊙O过点B交AB于点D,OE⊥AC,垂足为E,DE的延长线交BC的延长线于点F.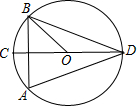 如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )
如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )