题目内容
【题目】如图,在正方形ABCD中,E是边AB的中点,F是边BC的中点,连结CE、DF.求证:CE=DF. 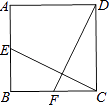
【答案】证明:∵ABCD是正方形, ∴AB=BC=CD,∠EBC=∠FCD=90°,
又∵E、F分别是AB、BC的中点,
∴BE=CF,
在△CEB和△DFC中,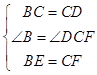 ,
,
∴△CEB≌△DFC,
∴CE=DF.
【解析】欲证明CE=DF,只要证明△CEB≌△DFC即可.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目