题目内容
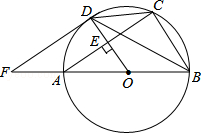
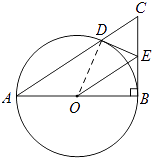
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE. 
(1)求证:DE是⊙O的切线.
(2)填空: ①当∠CAB=时,四边形AOED是平行四边形;
②连接OD,在①的条件下探索四边形OBED的形状为 .
【答案】
(1)解:连接OD,
∵E是BC的中点,
O是AB的中点,
∴OE是△ABC的中位线,
∴OE∥AC,
∠BOE=∠BAC,
∠DOE=∠ADO,
∵OD=OA,
∴∠BAC=∠ADO,
∴∠BOE=∠DOE,
在△DOE与△BOE中,
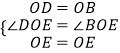 ,
,
∴△DOE≌△BOE,
∴∠OBE=∠ODE=90°,
∴DE是⊙O的切线
(2)45°;正方形
【解析】解:(2)①当∠CAB=45°时, ∴∠ADO=45°,
∴∠AOD=90°,
又∵∠EDO=90°,
∴DE∥AB,
∵OE∥AC,
∴四边形AOED是平行四边形;
②由①可知:∠EDO=∠DOB=∠ABC=90°,
∴四边形OBED是矩形,
∵OD=OB,
∴矩形OBED是正方形.
所以答案是:①45°;②正方形.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目