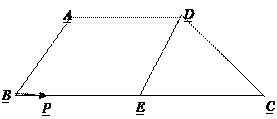题目内容
如图，在矩形ABCD中，AB=8，BC=6，E、F是AC的三等分点。则△BEF的面积为（ ）
| A．12 | B．8 | C．6 | D．无法计算 |
B
要求S△BEF只要求出底边EF以及EF边上的高就可以，高可以根据△ABC的面积得到，EF=
AC，根据勾股定理得到AC，就可以求出EF的长，从而求出△EFG的面积．
解：S△ABC=
×AB×BC=×8×6=24．
又E、F是AC上的三等分点．
∴S△BEF=S△ABC=8．
故选B．
点评：本题运用了勾股定理，已知直角三角形的两直角边，求斜边上的高，这类题的解决方法是需要熟记的内容．
AC，根据勾股定理得到AC，就可以求出EF的长，从而求出△EFG的面积．解：S△ABC=
×AB×BC=×8×6=24．又E、F是AC上的三等分点．
∴S△BEF=
S△ABC=8．故选B．
点评：本题运用了勾股定理，已知直角三角形的两直角边，求斜边上的高，这类题的解决方法是需要熟记的内容．
练习册系列答案
名校课堂系列答案
相关题目
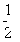S四边形ABCD
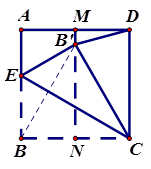
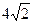cm，∠C=45°，点P从B点出发，沿着BC方向以1cm/s运动，到达点C停止，设P运动了ts。