题目内容
【题目】(题文)(1)阅读理解:
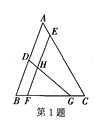
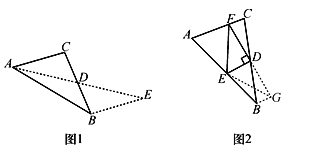
如图1,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是_________;
(2)问题解决:


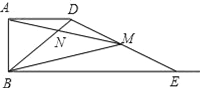
如图2,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证BE+CF>EF.
【答案】(1)2<AD<8(2)证明见解析
【解析】试题分析:(1)延长AD到E,使AD=DE,连接BE,△ADC≌△EDB,推出EB=AC,根据三角形的三边关系求出即可;
(2)先利用ASA判定△BGD≌△CFD,从而得出BG=CF;再利用全等的性质可得GD=FD,BG=CF,再有DE⊥DF,从而得出EG=EF,两边和大于第三边从而得出BE+CF>EF.
试题解析:(1)延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,
∴BD=CD,
在△ADC与△EDB中,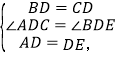
∴△ADC≌△EDB(SAS),
∴EB=AC,
根据三角形的三边关系得:ABAC<AE<AC+AB,
∴4<AE<16,
∵AE=2AD
∴2<AD<8,
即:BC边上的中线AD的取值范围2<AD<8;
故答案为:2<AD<8.
(2)BE+CF>EF.
理由:如图2,
过点B作![]() 交FD的延长线于G,
交FD的延长线于G,
∴∠DBG=∠DCF.
∵D为BC的中点,
∴BD=CD
又∵∠BDG=∠CDF,
在△BGD与△CFD中,
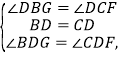
∴△BGD≌△CFD(ASA).
∴GD=FD,BG=CF.
又∵DE⊥DF,
∴EG=EF(垂直平分线到线段端点的距离相等).
∴在△EBG中,BE+BG>EG,
即BE+CF>EF.

【题目】小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 | ||
5≤x<6 | 10 | 20% |
6≤x<7 | 12% | |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
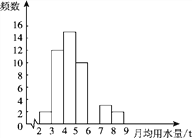
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
【题目】某教研部门为了了解在校初中生阅读教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读教科书情况统计图表
类别 | 人数 | 占总人数比例 |
重视 | a | b |
一般 | 57 | 0.285 |
不重视 | c | 0.36 |
说不清楚 | 9 | 0.045 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2500名,请估计该校“重视阅读教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读教科书的现状的看法及建议;
②如果要了解全省初中生阅读教科书的情况,你认为应该如何进行抽样?
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和告知给你代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写表格;
平均数/分 | 中位数/分 | 众数/分 | |
初中代表队 | |||
高中代表队 |
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.