Question

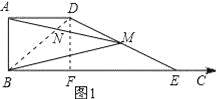
【题目】如图，已知AB=2，AD=4，∠DAB=90°，AD∥BC．E是射线BC上的动点（点E与点B不重合），M是线段DE的中点，连结BD，交线段AM于点N，如果以A，N，D为顶点的三角形与△BME相似，则线段BE的长为___________．

Answer 1

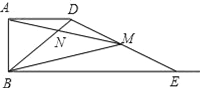
【答案】8或2

【解析】试题分析：因为如果三角形ADN和BME相似，一定不相等的角是∠ADN和∠MBE，因为AD∥BC，如果两角相等，那么M与D重合，显然不合题意，故应分两种情况进行讨论，设BE长为x．

①如图1，当∠ADN=∠BEM时，那么∠ADB=∠BEM，作DF⊥BE，垂足为F，tan∠ADB=tan∠BEM，AB：AD=DF：FE=AB：（BE﹣AD）．即2：4=2：（x﹣4）．解得x=8．即BE=8．

②如图2，当∠ADB=∠BME，而∠ADB=∠DBE，∴∠DBE=∠BME，∵∠E是公共角，

∴△BED∽△MEB，∴，BE2=DEEM=DE2=（DF2+EF2），

∴BE2=[22+（4﹣x）2]，∴x1=2，x2=﹣10（舍去），∴BE=2．

综上所述线段BE为8或2，

故答案为8或2．