题目内容
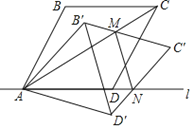
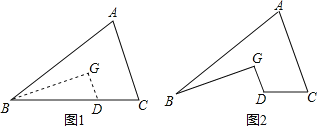
【题目】如图1,G为△ABC纸片的重心,DG∥AC交BC于点D,连结BG,剪去△BGD纸片,剩余部分纸片如图2所示,若原△ABC纸片面积为5,则图2纸片的面积为_____.
【答案】![]() .
.
【解析】
连接AG,延长AG交BD于E,设△DGE的面积为S,利用重心的性质和平行线分线段成比例,用S表示其它三角形的面积,最后得出S△ABC =18S=5,解得S![]() ,可得S△BDG=4S
,可得S△BDG=4S![]() ,即可得图2纸片的面积=5
,即可得图2纸片的面积=5![]() .
.
连接AG,延长AG交BD于E,如图1,设△DGE的面积为S,
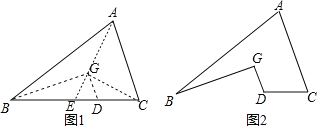
∵G为△ABC纸片的重心,
∴BE=CE,AG=2EG,
∵DG∥AC,
∴ED:DC=EG:AG=1:2,
∴S△DGC=2S△DEG=2S,
∴S△BEG=S△CEG=3S,
∴S△ABG=2S△BEG=6S,
∵S△ABE=3S+6S=9S,
∴S△ABC=2S△ABE=18S,
即18S=5,解得S![]() ,
,
∴S△BDG=4S![]() ,
,
∴图2纸片的面积=5![]() .
.
故答案为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.