题目内容
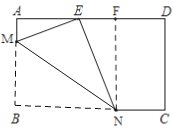
【题目】如图,已知矩形ABCD中,AB=6,AD=8将矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,如果AE=2AM,那么CN的长为______.
【答案】![]()
【解析】
如图,过N作NF⊥AD于F,可得NF=AB,根据矩形的性质和折叠的性质可得∠MEN=∠B=90°,EN=BN,根据直角三角形两锐角互余的性质及平角的定义可得∠AME=∠NEF,进而可证明△AEM∽△FNE,根据AE=2AM可求出EF的长,在Rt△FNE中,利用勾股定理可求出EN的长,进而可求出CN的长.
如图,过N作NF⊥AD于F,
∵四边形ABCD是矩形,AB=6,
∴NF=AB=6,
∵矩形ABCD沿直线MN翻折后,点B恰好落在边AD上的点E处,
∴EN=BN,∠MEN=∠B=90°,
∴∠AEM+∠NEF=90°,
∵∠AEM+∠AME=90°,
∴∠AME=∠NEF,
又∵∠A=∠EFN=90°,
∴△AEM∽△FNE,
∴![]() ,
,
∵AE=2AM,NF=6,
∴EF=3,
∴BN=EN=![]() =
=![]() =
=![]() ,
,
∵BC=8,
∴CN=BC-BN=8-![]() ,
,
故答案为:8-![]()

练习册系列答案
相关题目
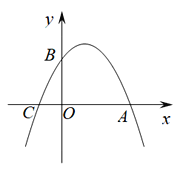
【题目】已知抛物线![]()
![]() 对称轴为______,顶点坐标为______;
对称轴为______,顶点坐标为______;
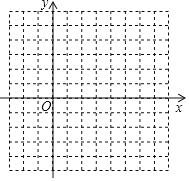
![]() 在坐标系中利用五点法画出此抛物线.
在坐标系中利用五点法画出此抛物线.
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
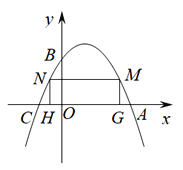
![]() 若抛物线与x轴交点为A、B,点
若抛物线与x轴交点为A、B,点![]() 在抛物线上,求
在抛物线上,求![]() 的面积.
的面积.