题目内容
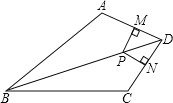
【题目】(本题满分10分)如图所示,BD平分∠ABC,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,M、N为垂足.求证:PM=PN.
【答案】见解析
【解析】
试题分析:根据条件证明△ABD≌△CBD得出∠ADD=∠CDB,然后利用角平分线的性质可得出结论.
试题解析:证法一:∵BD平分∠ABD,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
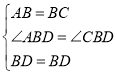
∴△ABD≌△CBD
∴∠ADD=∠CDB
∵PM⊥AD,PN⊥CD,
∴PM=PN.
证法二:∵BD平分∠ABD,
∴∠ABD=∠CBD.
在△ABD和△CBD中,
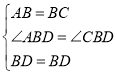
∴△ABD≌△CBD
∴∠ADD=∠CDB
∵PM⊥AD,PN⊥CD,
∴∠PND=∠PMD=90°
在△PMD和△PND中,
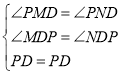
∴PM=PN.

练习册系列答案
相关题目