题目内容
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A(﹣3,0)和点B,与y轴交于点C(0,3),顶点为点D,对称轴DE交x轴于点E,连接AD,AC,DC.
(1)求抛物线的函数表达式.
(2)判断△ADC的形状,并说明理由.
(3)对称轴DE上是否存在点P,使点P到直线AD的距离与到x轴的距离相等?若存在,求出点P的坐标;若不存在,请说明理由.
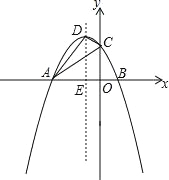
【答案】(1)抛物线解析式为y=﹣x2﹣2x+3;(2)
【解析】
试题分析:(1)用待定系数法求出抛物线解析式;
(2)先确定出抛物线的顶点坐标,从而求出AD,AC,CD,用勾股定理的逆定理判断即可;
(3)先求出∠ADE的正弦值,再分点P在∠DAB的平分线和∠DAB的外角的平分线两种情况用PM=PE建立方程求解即可.
试题解析:(1)∵点A(﹣3,0),C(0,3)在抛物线y=﹣x2+bx+c的图象上,
∴![]() ,∴
,∴![]() ,
,
∴抛物线解析式为y=﹣x2﹣2x+3,
(2)由(1)得抛物线解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的顶点D(﹣1,4),∵C(0,3),A(﹣3,0),
∴AD=2![]() ,AC=3
,AC=3![]() ,CD=
,CD=![]() ,∴AD2=AC2+CD2,
,∴AD2=AC2+CD2,
∴△ADC是直角三角形;
(3)存在,
理由:∵抛物线解析式为y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴E(﹣1,0),
∵A(﹣3,0),D(﹣1,4),
∴AE=2,DE=4,AD=2![]() ,
,
在Rt△ADE中,sin∠ADE=![]() =
=![]() ,
,
设P(﹣1,p),
∵点P到直线AD的距离与到x轴的距离相等
①当点P在∠DAB的角平分线时,
如图1,
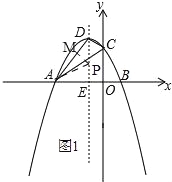
过点P作PM⊥AD,
∴PM=PD×sin∠ADE=![]() (4﹣p),PE=p,
(4﹣p),PE=p,
∵PM=PE,
∴![]() (4﹣p)=p,
(4﹣p)=p,
∴p=![]() ﹣1,
﹣1,
∴P(﹣1,![]() ﹣1),
﹣1),
②当点P在∠DAB的外角的平分线时,
如图2,
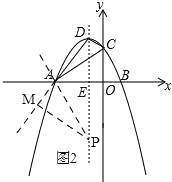
过点P作PM⊥AD,∴PM=PD×sin∠ADE=![]() (4﹣p),PE=﹣p,
(4﹣p),PE=﹣p,
∴![]() (4﹣p)=﹣p,∴p=﹣
(4﹣p)=﹣p,∴p=﹣![]() ﹣1,∴P(﹣1,﹣
﹣1,∴P(﹣1,﹣![]() ﹣1),
﹣1),
综上所述,存在点P到AD的距离与到x轴的距离相等,点P(﹣1,![]() ﹣1)或(﹣1,﹣
﹣1)或(﹣1,﹣![]() ﹣1).
﹣1).

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案