题目内容
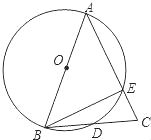
【题目】已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
(1)求∠EBC的度数;
(2)求证:BD=CD.
【答案】(1)22.5°.(2)证明见解析.
【解析】
试题分析:(1)∠EBC的度数等于∠ABC﹣∠ABE,因而求∠EBC的度数就可以转化为求∠ABC和∠ABE,根据等腰三角形的性质等边对等角,就可以求出.
(2)在等腰三角形ABC中,根据三线合一定理即可证得.
试题解析:(1)∵AB是⊙O的直径,
∴∠AEB=90°.
又∵∠BAC=45°,
∴∠ABE=45°.
又∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=22.5°.
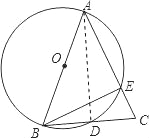
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
又∵AB=AC,
∴BD=CD.

练习册系列答案
相关题目
【题目】在一次体育达标测试中,九年级(3)班的15名男同学的引体向上成绩如下表所示:
成绩(个) | 8 | 9 | 11 | 12 | 13 | 15 |
人数 | 1 | 2 | 3 | 4 | 3 | 2 |
这15名男同学引体向上成绩的中位数和众数分别是( )
A.12,13
B.12,12
C.11,12
D.3,4