题目内容
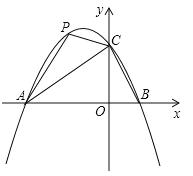
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)求直线AC的函数解析式;
(3)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2;(2)
x+2;(2)![]() ;(3)存在,(
;(3)存在,(![]() )
)
【解析】
(1)直接用待定系数法即可解答;
(2)先确定C点坐标,设直线AC的函数解析式y=kx+b,最后用待定系数法求解即可;
(3)连接PO,作PM⊥x轴于M,PN⊥y轴于N,然后求出△ACP面积的表达式,最后利用二次函数的性质求最值即可.
解:(1)∵抛物线y=ax2+bx+2过点A(﹣3,0),B(1,0),
∴![]()
解得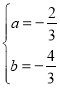 ,
,
∴二次函数的关系解析式为y=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;
(2)∵当x=0时,y=2,
∴C(0,2)
设直线AC的解析式为![]() ,把A、C两点代入得
,把A、C两点代入得
![]() 解得
解得![]()
∴直线AC的函数解析式为![]() ;
;
(3)存在.
如图: 连接PO,作PM⊥x轴于M,PN⊥y轴于N
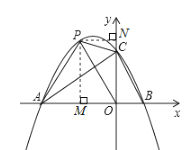
设点P坐标为(m,n),则n=![]() ),PN=-m,AO=3
),PN=-m,AO=3
当x=0时,y=![]() =2,
=2,
∴点C的坐标为(0,2),OC=2
∵![]()
![]()
=![]()
∵a=-1<0
∴函数S△PAC=-m2-3m有最大值
∴b当m=![]()
∴当m=![]() 时,S△PAC有最大值n=
时,S△PAC有最大值n=![]()
∴当△ACP的面积最大时,P的坐标为(![]() ).
).

 口算题天天练系列答案
口算题天天练系列答案【题目】某厂的四台机床同时生产直径为![]() 的零件,为了了解产品质量,质量检验员从这四台机床生产的零件中分别随机抽取50件产品,经过检测、整理、描述与分析,得到结果如下(单位:
的零件,为了了解产品质量,质量检验员从这四台机床生产的零件中分别随机抽取50件产品,经过检测、整理、描述与分析,得到结果如下(单位:![]() ):
):
特征数 机床 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 9.99 | 9.99 | 10.00 | 0.02 |
乙 | 9.99 | 10.00 | 10.00 | 0.07 |
丙 | 10.02 | 10.01 | 10.00 | 0.02 |
丁 | 10.02 | 9.99 | 10.00 | 0.05 |
从样本来看,生产的零件直径更接近标准要求且更稳定的机床是( )
A.甲B.乙C.丙D.丁