��Ŀ����
����Ŀ��������ʦ��������ޱޱ����ͬѧ��������Զ��������β��ԣ�����Ϊ10�֣��������ǵijɼ����Ƴ�����ͳ��ͼ.����ͼ����Ϣ������˵����ȷ���ǣ� ��
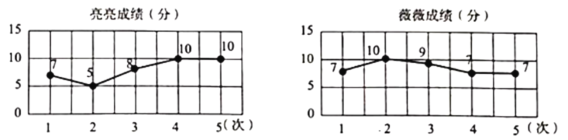
A.��������Զ�ɼ���ޱޱ����Զ�ɼ��ȶ�
B.�����ijɼ�Խ��Խ�ã��������һ��һ������10��
C.�����ĵ����γɼ���ڶ��γɼ���ȣ������ʳ���![]()
D.������ޱޱ�ijɼ�����8�����²����������˵ijɼ��ȶ���һ��
���𰸡�C
��������
A.���ݲ���ͳ��ͼ��ֱ�۹۲�����жϼ��ɣ�
B. ������Զ�ɼ���������ԣ��������һ�β�һ������10�֣��ʿɶ�B�����жϣ�
C����������ʼ��ɵó����ۣ�
D.�ֱ���������ɵó����ۣ�
A.����������ͼ����ֱ�ۿ���ޱޱ����Զ�ɼ����ȶ����ʴ�ѡ�����
B.������Զ�ɼ���������ԣ��������һ�β�һ������10�֣��ʴ�ѡ�����
C.�����ĵ����γɼ���ڶ��γɼ���ȣ�������Ϊ![]() ���ʴ�ѡ����ȷ��
���ʴ�ѡ����ȷ��
D. ������ƽ���ɼ�Ϊ��![]() ���֣���
���֣���
������![]() ��
��
ޱޱ��ƽ���ɼ�Ϊ��![]() ���֣���
���֣���
������![]()
��ޱޱ�ɼ��ķ���С�������ɼ��ķ��
��ޱޱ�ijɼ��Ƚ��ȶ�����ѡ��D����
��ѡC��

 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�����Ŀ��������ȫ�潨��С�����͡�ʮ���塱�滮�չ�֮�꣬Ϊ�ٽ����ۣ�ij��˾������A��B�����²�Ʒ������ǰ����������֪A��B�ijɱ����ۼۺ�ÿ���������±���ʾ��
�ɱ���Ԫ/���� | �ۼۣ�Ԫ/���� | ��������/�գ� | |
A | 500 | 700 | 500 |
B | 800 | 1050 | 300 |
���������������˾��B���Ʒ�������ۣ�ͬʱ��A���Ʒ������ۣ�����B���Ʒÿ����5Ԫ�Ͷ�����2����A���Ʒÿ���5Ԫ�Ϳ�������1����Ҫ����ÿ�յ����������䣬��A���Ʒÿ��������x����ÿ���ܻ���ΪyԪ��
��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2��Ҫʹÿ��������208000Ԫ��ֱ��д��x��ȡֵ��Χ��
��3���ù�˾����ÿ����һ��A��Ʒ���;����ʮ�ֻ�a��0��a��100��Ԫ��Ϊ�����𣮵�40��x��50ʱ��ÿ�յ��������Ϊ237250Ԫ����a��ֵ��
����Ŀ�������Ŭ����������2019���������������ͬ�����ơ����������ϳ�����������������£�����������ϸ�����![]() ����������Ҫ��Ⱦ��ͬ�Ⱦ����Ը��ƶԱ����п����������й����ݽ����ռ����������������������������˲�����Ϣ��
����������Ҫ��Ⱦ��ͬ�Ⱦ����Ը��ƶԱ����п����������й����ݽ����ռ����������������������������˲�����Ϣ��
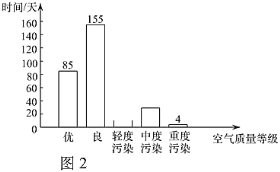
a��������2019���������������ֲ��������ͼ��ȫ����������Ⱦ�գ�������������

b��������2019����������ж�������![]() �������Ũ��Ϊ4��/�����ף��ȶ��ﵽ���Ҷ�������60��/�����ף���
�������Ũ��Ϊ4��/�����ף��ȶ��ﵽ���Ҷ�������60��/�����ף���![]() ������������
������������![]() �������Ũ���ֱ�Ϊ68��/�����ף�37��/�����ף����״δﵽ���Ҷ�������70��/�����ף�40��/�����ף���
�������Ũ���ֱ�Ϊ68��/�����ף�37��/�����ף����״δﵽ���Ҷ�������70��/�����ף�40��/�����ף���![]() �����Ũ��Ϊ
�����Ũ��Ϊ![]() �������ף����DZ����д�����Ҫ��Ⱦ��������Ҷ�������35��/�����ף���20%��
�������ף����DZ����д�����Ҫ��Ⱦ��������Ҷ�������35��/�����ף���20%��
c��������2019�����������![]() �¾�Ũ�ȱ仯������£�
�¾�Ũ�ȱ仯������£�
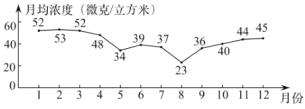
��������![]() ���¾�Ũ������λ����/�����ף����£�����������
���¾�Ũ������λ����/�����ף����£�����������
�·� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
�¾�Ũ�� | 9 | 6 | 5 | 4 | 3 | 2 | 3 | 3 | 5 | 4 |
������������Դ�ڱ�������̬�����ֹٷ���վ��
���������ţ��ش��������⣺
��1��������2019���������Ϊ�������Ⱦ������Ϊ�� ����
A��82 B��92 C��102
��2��![]() ��ֵ��______��
��ֵ��______��
��3��������2019�����������![]() �¾�Ũ���ﵽ���Ҷ������ĸ���Ϊ______��
�¾�Ũ���ﵽ���Ҷ������ĸ���Ϊ______��
��4��������2019�����������![]() �¾�Ũ����������4������λ����______��
�¾�Ũ����������4������λ����______��
����Ŀ��ij������ij��б�ҵ��ѧ���ԣ��⽫��������������Ϊ�����������Ե�һ���ؿ���Ŀ������Ϊ10�֣��йز���Ϊ��ǰ�˽�����μӳ��б�ҵ��ѧ���Ե�������������������ˮƽ����ȫ�а��꼶�����������ȡ�˲��������������ǵ�������������ˮƽ���в��ԣ��������Խ�����Ƴ�����ͳ��ͼ����������Ϣδ��������
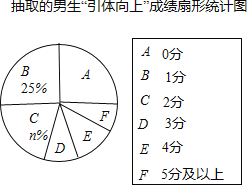
�������ͳ��ͼ���е���Ϣ������������⣺
��ȡ�������������������ɼ�ͳ�Ʊ�
�ɼ� | ���� |
0�� | 32 |
1�� | 30 |
2�� | 24 |
3�� | 11 |
4�� | 15 |
5�ּ����� | m |
��1����գ�m���� ����n���� ����
��2��������ͳ��ͼ��D�������Բ�ĽǵĶ�����
��3��Ŀǰ���а��꼶������3600�����������������������������ֵ�������
����Ŀ��������2��27�չ���Ժ�������ŷ������ϣ��й��������ķ������ᵽ�������¹ڷ��ͷ������������������֣���ij��λ�������ɹ���һ��ҽ����ƿ��֣����۷ֱ�Ϊ1Ԫ��1.5Ԫ��3Ԫ��5Ԫ��10Ԫ��ÿ������䷢��ÿλ�ڸ�Ա��һ������.�ֽ�����10������䷢��������Ƴ�����ͳ�Ʊ���
�䷢��/�� | 30 | 25 | 20 | 15 |
����/�� | 2 |
|
| 1 |
��֪�䷢����ƽ������23������λ����![]() ����������
����������![]() ����
����
��1����![]() ��ֵ��������
��ֵ��������![]() ��
��
��2�����䷢15��������һ���в�ͬ�ͺŵĿ��ַ����������ͳ�ƣ����Ƴ���ͼ��ʾ���в�������ͳ��ͼ.��ȫͳ��ͼ������С����ò�����3Ԫ���ֵĸ��ʣ�
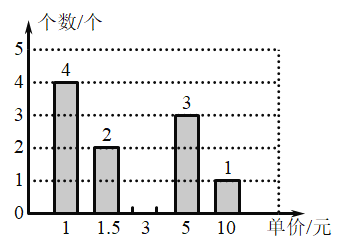
��3������������������֣�����12������䷢����������ǰ10������䷢����������ͬ�����磺ֻҪ�ڵ�11�죬��12�춼����30�����֣�����12����ַ�����������Ϊ30����20������д����12������䷢����������������ʾ�����������������