题目内容
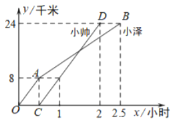
【题目】小泽和小帅两同学分别从甲地出发，骑自行车沿同一条路到乙地参加社会实践活动．如图折线
和线段
分别表示小泽和小帅离甲地的距离
（单位：千米）与时间
（单位：小时）之间函数关系的图象，则当小帅到达乙地时，小泽距乙地的距离为_________千米．
【答案】4
【解析】
由图象，通过点（1，8）和点（2，24）直线CD的解析式，求点C的横坐标，即可求出点A的坐标，从而可以求出直线AB的函数解析式，小帅到达乙地的时间为2小时，则将x=2代入直线AB解析式即可知此时小泽的位置，从而可以求出当小帅到达乙地时，小泽距乙地的距离．
解：由图象可得，点（1，8）和点（2，24）在直线CD上，设直线CD的解析式为：y1=kx+b
代入得，
，解得
，
∴y1=16x-8
∴当y=0时，0=16x-8，解得，x=
∴点C（，0）点A（，8）
∵点A（，8），点B（2.5，24）在直线AB上，
∴设直线AB的解析式为：y2=kx+b
代入得
，
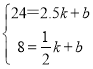解得
∴y2=8x+4
∴当x=2时，y2=8×2+4=20，
∴此时小泽距离乙地的距离为：24-20=4千米
故答案为：4
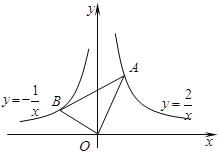
【题目】有这样一个问题：探究函数y＝
的图象与性质．小彤根据学习函数的经验，对函数y＝的图象与性质进行了探究．
下面是小彤探究的过程，请补充完整：
(1)函数y＝的自变量x的取值范围是 ；
(2)下表是y与x的几组对应值：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | … |
y | … |
| m |
| 0 | ﹣1 | 3 | 2 |
|
|
| … |
则m的值为 ；
(3)如图所示，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出了图象的一部分，请根据剩余的点补全此函数的图象；
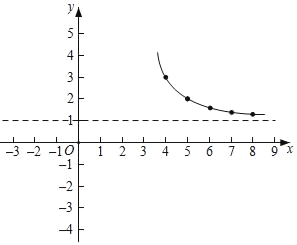
(4)观察图象，写出该函数的一条性质 ；
(5)若函数y＝的图象上有三个点A(x1，y1)、B(x2，y2)、C(x3，y3)，且x1＜3＜x2＜x3，则y1、y2、y3之间的大小关系为 ；
【题目】某家庭记录了未使用节水龙头50天的日用水量(单位：m3)和使用了节木龙头50天的日用水量，得到频数分布表如下：
表1未使用节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 | 0.6≤x≤0.7 |
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
表2使用了节水龙头50天的日用水量频数分布表
日用水量x | 0≤x<0.1 | 0.1≤x<0.2 | 0.2≤x<0.3 | 0.3≤x<0.4 | 0.4≤x<0.5 | 0.5≤x<0.6 |
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)估计该家庭使用节水龙头后，日用水量小于0.3 m3的概率；
(2)估计该家庭使用节水龙头后，一年能节省多少水?(一年按365天计算，同一组中的数据以这组数据所在范围的组中值作代表.)
