Question

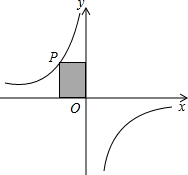
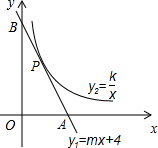
如图，直线y₁=mx+4与x轴、y轴分别交于A点、B点，且与反比例函数y₂=

k

x

在第一象限的图象有唯一的公共点P，若S_△OAB=4，则k=______．

Answer 1

对于直线y₁=mx+4，
令x=0，解得：y=4，故B（0，4），即OB=4，
∵S_△OAB=

1

2

OA•OB=

1

2

×4OA=4，
∴OA=2，即A（2，0），
将A坐标代入y₁=mx+4得：0=2m+4，即m=-2，
∴y₁=-2x+4，
将两函数解析式联立得：

y=-2x+4 y= k x

，
消去y得：-2x+4=

k

x

，即2x²-4x+k=0，
∵两函数在第一象限的图象有唯一的公共点P，
∴b²-4ac=16-8k=0，
解得：k=2．
故答案为：2