题目内容
【题目】如图是抛物线型拱桥,当拱顶离水面![]() 时,水面宽
时,水面宽![]() 为
为![]() .当水面上升
.当水面上升![]() 时达到警戒水位,此时拱桥内的水面宽度是多少
时达到警戒水位,此时拱桥内的水面宽度是多少![]() ?
?
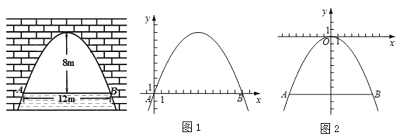
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1.以点![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,此时点
,此时点![]() 的坐标为_______,抛物线的项点坐标为_______,可求这条抛物线所表示的二次函数解析式为_______.当
的坐标为_______,抛物线的项点坐标为_______,可求这条抛物线所表示的二次函数解析式为_______.当![]() 时,求出此时自变量
时,求出此时自变量![]() 的取值,即可解决这个问题.
的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为![]() 轴.建立平面直角坐标系
轴.建立平面直角坐标系![]() ,这时这条抛物线所表示的二次函数的解析式为_______,当水面达到警戒水位,即
,这时这条抛物线所表示的二次函数的解析式为_______,当水面达到警戒水位,即![]() _______时,求出此时自变量
_______时,求出此时自变量![]() 的取值为_______,从而得水面宽为
的取值为_______,从而得水面宽为![]() .
.
【答案】(12,0);(6,8);![]() ;y=
;y=![]() x2;-2;±3.
x2;-2;±3.
【解析】
方法一:根据顶点坐标为(6,8),设其解析式为y=a(x-6)2+8,将(0,0)代入求出a的值即可得;
方法二:设抛物线解析式为y=ax2,将点(6,-8)代入求得a的值,据此可得抛物线的解析式,再求出上涨6m后,即y=-2时x的值即可.
方法一:根据题意可得:
B点的坐标为(12,0),顶点坐标为(6,8),
设二次函数的解析式为y=a(x-6)2+8,
把A(0,0)代入得,![]() ,a=
,a=![]() ,
,
∴二次函数的解析式为![]() ;
;
方法二:设二次函数的解析式为y=ax2,
把B(6,-8)代入得,a=![]() ,
,
∴二次函数的解析式为y=![]() x2;
x2;
y=-2时,求出此时自变量x的取值为±3,
故答案为:(12,0);(6,8);![]() ;y=
;y=![]() x2;-2;±3.
x2;-2;±3.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目