题目内容
两组邻边分别相等的四边形我们称它为菱形.
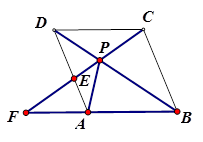
如图,在菱形 中,
中, ,
, ,
, ,
, 相交于点
相交于点 ,
,

(1)求证:① ;
;
② ,
, ;
;
(2)如果 ,
, ,求菱形
,求菱形 的面积.
的面积.
如图,在菱形
 中,
中, ,
, ,
, ,
, 相交于点
相交于点 ,
,
(1)求证:①
 ;
;②
 ,
, ;
;(2)如果
 ,
, ,求菱形
,求菱形 的面积.
的面积.(1)见解析(2)12
证明:(1)①在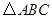 和
和 中,
中,
 ,
, ,
,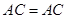 ,····················· 2分
,····················· 2分
 .···························· 3分
.···························· 3分
②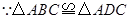 ,
,
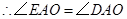 .···························· 4分
.···························· 4分
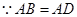 ,
,
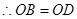 ,
, .························· 6分
.························· 6分
(2)菱形 的面积
的面积
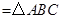 的面积+
的面积+ 的面积
的面积
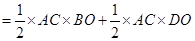
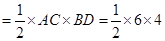
 .
.
(1)找出两三角形的三边分别对应相等,根据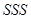 可知三角形全等,利用全等三角形对应角相等,根据等腰三角形三线合一即可
可知三角形全等,利用全等三角形对应角相等,根据等腰三角形三线合一即可
(2)把菱形 的面积转化成
的面积转化成 的面积与
的面积与 的面积的和即可
的面积的和即可
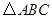 和
和 中,
中, ,
, ,
,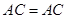 ,····················· 2分
,····················· 2分 .···························· 3分
.···························· 3分②
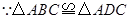 ,
,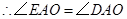 .···························· 4分
.···························· 4分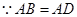 ,
,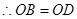 ,
, .························· 6分
.························· 6分(2)菱形
 的面积
的面积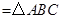 的面积+
的面积+ 的面积
的面积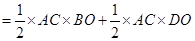
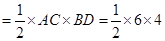
 .
.(1)找出两三角形的三边分别对应相等,根据
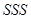 可知三角形全等,利用全等三角形对应角相等,根据等腰三角形三线合一即可
可知三角形全等,利用全等三角形对应角相等,根据等腰三角形三线合一即可(2)把菱形
 的面积转化成
的面积转化成 的面积与
的面积与 的面积的和即可
的面积的和即可
练习册系列答案
相关题目
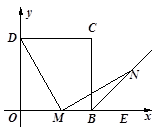
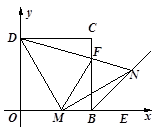
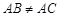 ,D是边BC上的一点,DE∥CA交AB于点E, DF∥BA交AC于点F. 要使四边形AEDF是菱形,只需添加条件
,D是边BC上的一点,DE∥CA交AB于点E, DF∥BA交AC于点F. 要使四边形AEDF是菱形,只需添加条件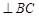
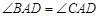
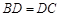
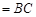
 中,
中, ,
, 为
为 中点,
中点,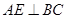 ,
, 于点
于点 ,
,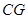 ∥
∥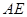 ,
, 于点
于点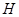 ,交
,交 于点
于点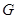 .
. 的度数.
的度数.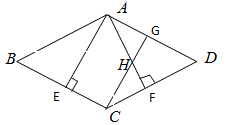


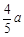
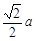
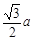
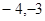 ),D(6,
),D(6,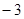 ),并将各点用线段一次连接构成一个四边形ABCD。
),并将各点用线段一次连接构成一个四边形ABCD。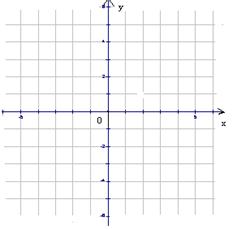
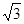 ,P是线段AC上的一个动点.
,P是线段AC上的一个动点.
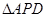 全等的三角形,并说明理由;
全等的三角形,并说明理由;